Junhyuk Yu

I will be an amazing person.

해당 내용은 ‘파이썬 알고리즘 인터뷰’ 책의 일부를 발췌하여 정리한 내용입니다.

비트 조작

비트를 조작하는 것은 하드웨어와 관련이 깊다. 현대의 모든 디지털 컴퓨터의 기본 개념이자 근간을 이루고 있는 논리 회로(Logic Circuit)는 True, False 2개의 값으로 논리 연산을 설명하는 부울대수(Boolean Algebra)를 전기회로 스위치의 on/off에 적용시켰다. 현대에 이르러 비트 조작 기법은 하드웨어 뿐만 아니라 다양한 부분에서 활용되고 있다.

부울 연산자(Boolean Operation)

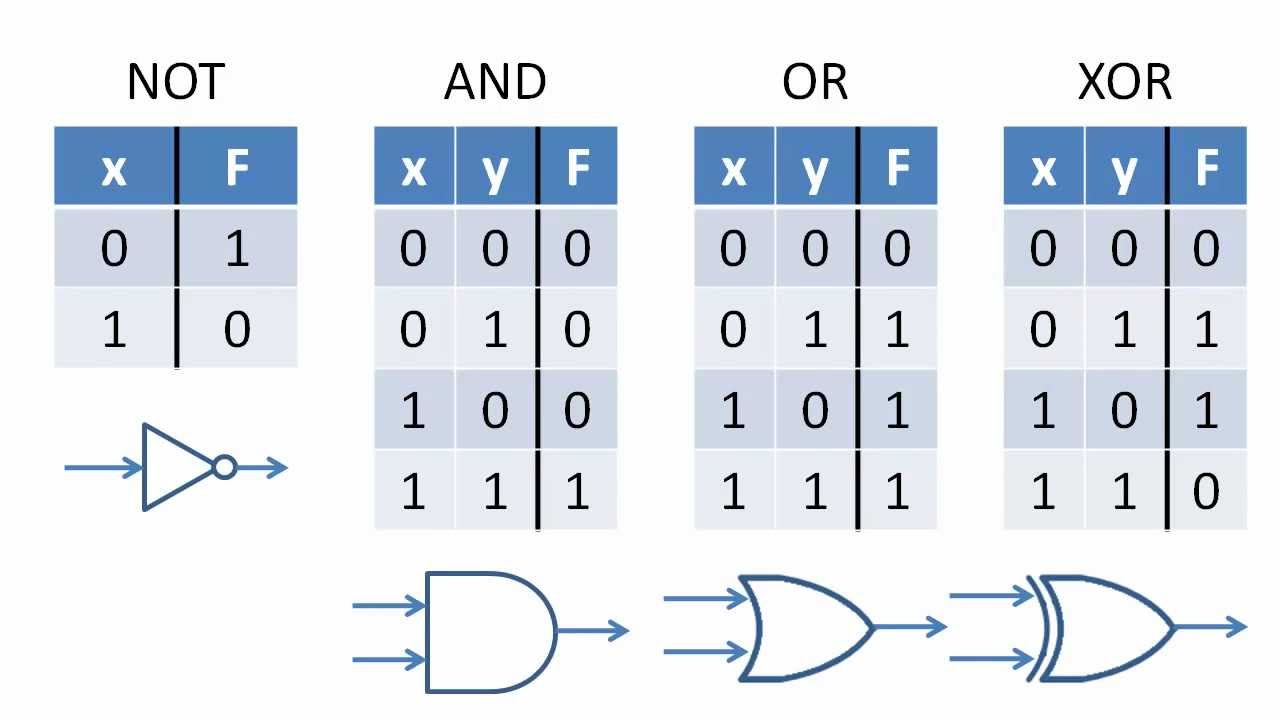
출처 : Boolean Operators

# 기본 부울 연산자
>>> True and False
False
>>> True or False
True
>> not True
False

AND, OR, NOT은 기본 부울 연산자로, 연산들의 다양한 조합을 통해 보조 연산을 만들어 낼 수 있으며, 가장 대표적인 보조 연산이 XOR이다. XOR은 디지털 논리 게이트에서 매우 중요한 위치를 차지한다.

# XOR 연산자
>>> x = y = True
>>> (x and not y) or (not x and y)
False

비트 연산자(Bitwise Operator)

# AND
>>> True & False
False
# OR
>>> True | False
True
# XOR
>>> True ^ True
False
# NOT
>>> ~ True
-2

NOT 연산에서는 부울 변수에 적용하면 True는 1로 간주되어 -2가 된다. 비트 연산자 NOT은 2의 보수에서 1을 뺀 값과 같기 때문이다. 따라서 십진수로 표현할 때는 NOT x = -x - 1이 되어 NOT 1 = -1 -1이 되어 -2가 된다.

비트 조작 퀴즈

다음은 산술 연산(arithmetic Operation)을 비롯한 몇 가지 비트 연산을 살펴보자.

# bin(number) : 
# 전달받은 interger 혹은 long integer 자료형의 값을 이진수 문자열로 돌려준다. 
# 0b는 이진수를 의미하는 접두사이다.

>>> bin(0b0110 + 0b0010)
'0b1000'
>>> bin(0b0011 * 0b0101)
'0b1111'

덧셈과 곱셉은 십진수의 계산과 동일하다.

>>> bin(0b1101 >> 2)
'0b11'
>>> bin(0b1101 << 2)
'0b110100'

<<와 >>은 시프팅이다. >> 2은 오른쪽으로 2칸 시프팅을 의미한다. 반면, << 2은 왼쪽으로 2칸 시프팅을 의미하며, 뒷쪽에 0이 2개 붙는다. 십진수로 치면 2배씩 증가하는 것과 같다.

>>> bin(0b0101 ^ ~0b1100)
'-0b1010'

~0b1100은 0b0011이 되고 따라서 0b0101 ^ 0b0011 = 0b0110을 기대하였으나, 실제 값은 -0b1010이 나왔다. 그 이유는 뭘까? 앞서, 비트 연산자 NOT 결과는 십진수로 NOT x = -x -1이고 2의 보수에서 1을 뺀 결과값이라고 설명하였다. 그렇다면 0b1100의 십진수는 12이기에 -12 -1 = -13이 된다. 이 값 때문에 우리가 예상했던 값과 다른 결과값이 나오게 되는 것이다. 그렇다면 어떤 방식으로 우리가 원하는 연산 결과를 만들어 낼 수 있을까? 자릿수 만큼 최대값을 지닌 비트 마스크를 만들고, 그 값과 XOR을 통해 값을 만들어 본다.

>>> bin(0b1100 ^ 0b1111)
'0b11'

그렇다면 다음과 같이 Mask와 XOR결과를 처리하는 형태로 수정할 수 있다.

>>> MASK = 0b1111
>>> bin(0b0101 ^ (0b1100 ^ MASK))
'0b110'

🔠 파이썬의 진법 표현

# bin을 이용해서 이진수로 표현
>>> bin(87)
'0b1010111'
# int를 이용해서 십진수로 표현
>>> int('0b1010111', 2)
87
# 접두사 생력도 가능
>>> int('1010111', 2)
87

2의 보수(Two’s Complement)

2의 보수 숫자 포맷

2의 보수는 컴퓨터가 음수를 저장하기 위해 일반적으로 취하는 여러 방법 중 하나이다. 계산의 편의를 위해 4비트로 숫자 표현을 해보도록 한다.

출처 : DARKER THAN BLACK 黒の契約者

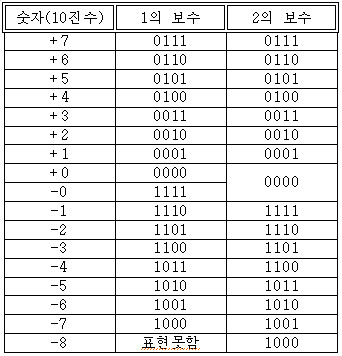
2의 보수 수학 연산

2의 보수 수학 연산은 가산 역 연산(Additive Inverse Operation)이라 부를 수 있다. 간단하게, 양수를 음수로, 음수를 양수로 바꾸는 작업을 말한다. 방법은 다음과 같다.

  1. ‘비트 연산자 NOT’은 2의 보수에서 1을 뺀 것이고,
  2. ‘2의 보수 수학 연산’은 비트 연산자 NOT에서 1을 더한 것이다.

0111의 2의 보수 연산은 1000 + 1 = 1001이 된다. 1001의 비트 연산자 NOT은 0111 - 1 = 0110이다. 이 값은 ~1001로 표현하기도 한다.

싱글 넘버

딱 하나를 제외하고 모든 엘리먼트는 2개 씩 있다. 1개인 엘리먼트를 찾아라.

Input: nums = [2,2,1]
Output: 1
---
Input: nums = [4,1,2,1,2]
Output: 4
---
Input: nums = [1]
Output: 1
  • 풀이: XOR 풀이
class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        result = 0
        for num in nums:
            result ^= num

        return result

XOR은 입력값이 서로 다르면 True, 동일하면 False를 출력한다. result ^= num을 통해, 만약 result와 num이 다른 값이라면 result는 num의 값을 가지게 된다. 이후, 동일한 num값을 만나게 되면 0으로 초기화가 된다. 이러한 방식으로 문제를 풀이할 수 있다.

You may also enjoy