알고리즘 - 다이나믹 프로그래밍 l
해당 내용은 ‘파이썬 알고리즘 인터뷰’ 책의 일부를 발췌하여 정리한 내용입니다.
다이나믹 프로그래밍(Dynamic Programming)
다이나믹 프로그래밍 알고리즘은 응용 수학자 리차드 밸만이 1953년에 고안한 알고리즘으로 문제를 각각의 작은 문제로 나누어 해결한 결과를 저장해둿다가 나중에 큰 문제의 결과와 합하여 풀이하는 알고리즘이다. 최적 부분 구조를 갖는 문제를 풀이하는데 있어 그리디 알고리즘과 비교 대상이 되는데, 그리디는 항상 그 순간에 최적이 되는 것 위주로 풀이가 된다면 다이나믹 프로그래밍은 중복된 하위 문제들(Overlapping Subproblem)의 결과를 저장해뒀가가 풀이해 나간다는 차이가 있다.
| 알고리즘 | 풀이 가능한 문제들의 특징 | 풀이 가능한 문제 및 알고리즘 | | — | — | — | | 다이나믹 프로그래밍 | 최적 부분 구조 중복된 하위 문제들 | 0-1 배낭 문제 피보나치 수열 다익스트라 알고리즘 | | 그리디 알고리즘 | 최적 부분 구조 탐욕 선택 속성 | 분할 가능 배낭 문제 다익스트라 알고리즘 | | 분할 정복 | 최적 부분 구조 | 병합정렬 퀵 정렬 |
최적 부분 구조
예를 들어, A에서 C까지 가는 최단 거리를 구하는 문제가 있다고 하자. 이중 A에서 B로 가는 각기 다른 3가지 경로가 존재하고, B에서 C까지 가는 각기 다른 3가지 경로가 있다. 그렇다면, A에서 C까지의 최단 거리는 (A에서 B까지 최단거리) + (B에서 C까지 최단거리)가 된다. 즉, 각 경로의 최단 경로 문제의 해결 방법의 합이다. 따라서 문제의 최적 해결 방법은 부분 문제에 대한 최적 해결 방법으로 구성된다.
이러한 구조를 최적 부분 구조라 하며, 분할 정복으로도 풀이가 가능하고 다이나믹 프로그래밍 또는 그리디 알고리즘으로 접근해볼 수 있는 문제다. 그러나, 만약 A에서 C까지 가는 터널이 뚫려 더 이상 B를 경유하지 않아도 된다면 이 문제는 더 이상 최적 구조 부분 구조가 아니게 된다.
중복된 하위 문제들
다이나믹 알고리즘으로 풀 수 있는 문제들과 다른 문제들의 결정적인 차이는 중복된 하위 문제들을 갖는다는 점이다. 가장 대표적으로 피보나치 수열 문제가 있다. 피보나치 수열을 재귀로 풀면 반복적으로 동일한 하위 문제들이 발생하며 이 부분이 핵심이다. 중복 문제가 발생하지 않는 병합 정렬은 분할 정복으로 분류되지만, 피보나치 수열 풀이는 다이나믹 프로그래밍 대상으로 분류된다.
다이나믹 프로그래밍 방법론
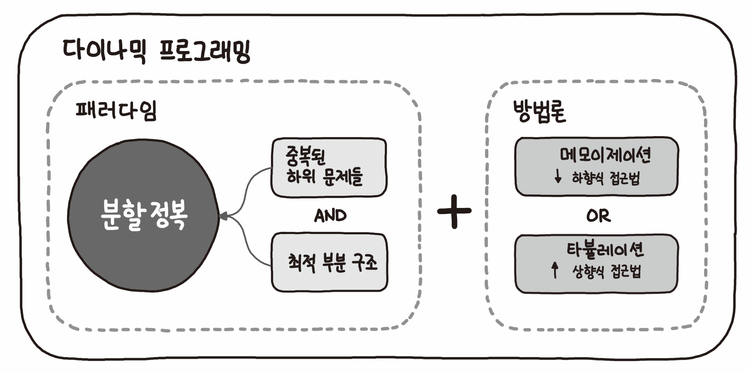
- 상향식 : 더 작은 하위 문제부터 살펴 본 다음, 작은 문제의 정답을 잉요해 큰 문제의 정답을 풀어나간다. 일반적으로 다이나믹 프로그래밍으로 지칭하기도 한다.
- 하향식 : 하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 자연스러운 방식으로 풀어나간다.
피보나치 수
피보나치 수를 구하라.
Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
---
Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
---
Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
- 풀이: 재귀 구조 브루트 포스
class Solution:
def fib(self, N: int) -> int:
if N <= 1:
return N
return self.fib(N - 1) + self.fib(N - 2)
풀이가 가능하나, 시간이 매우 오래 걸린다. 최적화를 진행해보자.
- 풀이: 메모이제이션
class Solution:
dp = collections.defaultdict(int)
def fib(self, N: int) -> int:
if N <= 1:
return N
if self.dp[N]:
return self.dp[N]
self.dp[N] = self.fib(N - 1) + self.fib(N - 2)
return self.dp[N]
재귀 구조를 사용하며, 계산한 값은 미리 저장해두기 때문에 매우 효율적이다.
- 풀이: 타뷸레이션
class Solution:
dp = collections.defaultdict(int)
def fib(self, N: int) -> int:
self.dp[0] = 0
self.dp[1] = 1
for i in range(2, N + 1):
self.dp[i] = self.dp[i - 1] + self.dp[i - 2]
return self.dp[N]
재귀를 사용하지 않고 반복으로 풀이하며, 작은 값부터 직접 계산한다. 일차원 선형 구조라 복잡하지 않고, 구조 차제도 단순해 이해하기 쉬우며 빠르기까지 하다.
- 두 변수만 이용해 공간 절약
class Solution:
def fib(self, N: int) -> int:
x, y = 0, 1
for i in range(0, N):
x, y = y, x + y
return x
매소드 바깥에 클래스으의 멤버 변수 선언도 필요가 없기 때문에 코드가 훨씬 더 간결해지며, 공간 복잡도도 O(n)에서 O(1)로 줄어든다.
0-1 배낭 문제
다이나믹 프로그래밍의 대표적인 문제 중 하나이다. 자세한 내용은 해당 링크를 참고하자.
최대 서브 배열
합이 최대가 되는 연속 서브 배열을 찾아 합을 리턴하라.
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The subarray [4,-1,2,1] has the largest sum 6.
---
Input: nums = [1]
Output: 1
Explanation: The subarray [1] has the largest sum 1.
---
Input: nums = [5,4,-1,7,8]
Output: 23
Explanation: The subarray [5,4,-1,7,8] has the largest sum 23.
- 풀이: 메모이제이션
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
for i in range(1, len(nums)):
nums[i] += nums[i - 1] if nums[i - 1] > 0 else 0
return max(nums)
- 풀이: 카데인 알고리즘
원래 이 문제는 1977년에 제안된 매우 유명한 컴퓨터 과학 알고리즘 문제로서, 제이 카데인이 O(n)에 풀이가 가능하도록 고안한 알고리즘이다.
from typing import List
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
best_sum = -sys.maxsize
current_sum = 0
for num in nums:
current_sum = max(num, current_sum + num)
best_sum = max(best_sum, current_sum)
return best_sum
