비선형 자료구조 - 그래프 l
해당 내용은 ‘파이썬 알고리즘 인터뷰’ 책의 일부를 발췌하여 정리한 내용입니다.
비선형(Non-Linear) 자료 구조는 선형과 달리 멀티 레벨로 구성된다(트리를 떠올리면 된다.). 탐색이 복잡하고 선형에 비해 구현이 복잡하지만, 메모리를 효율적으로 사용할 수 있다는 장점이 있다.
그래프
수학에서, 좀 더 구체적으로 그래프 이론에서 그래프란 객체의 일부 쌍(pair)들이 ‘연관되어’ 있는 객체 집합 구조를 말한다.
오일러 경로
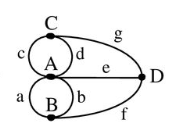
300여 년 전 프로이센 공국의 쾨니히스베르크에는 프레겔 강이 흐르고 있었다. 강에는 2개의 큰 섬이 있고 섬과 도시를 연결하는 7개의 다리가 놓여있었다. ‘그래프 이론’의 시작은, 이 7개 다리를 한 번씩만 건너서 모두 지나갈 수 있는지에 대한 풀이에서 시작되었다. 레온하르트 오일러가 이 문제에 대한 해결법을 논문에서 제시하였고 100년 이상 뒤에 수학적으로 증명이 되면서 이를 ‘오일러 정리’라고 부른다. 오일러는 A부터 D까지를 정점(Vertex), a부터 f까지를 간선(Edge)로 구성된 수학적 구조에서 모든 정점이 짝수 개의 차수(Degree)를 갖는다면 모든 다리를 한 번씩만 건너서 도달하는 것이 가능하다고 설명하였다. 한번도 붓을 떼지 않고 모든 간선을 한번 씩만 그릴 수 있는 ‘한붓 그리기’로 이해하면 쉽다.
해밀턴 경로
해밀턴 경로는 각 정점을 한 번씩 방문하는 무향 또는 유향 그래프 경로를 말한다.
해밀턴 경로와 오일러 경로의 차이점은 오일러는 경로는 간선을, 해밀러는 정점을 기준으로 한다는 점이다. 하지만, 놀랍게도 해밀턴 경로를 찾는 문제는 최적 알고리즘이 없는 대표적인 NP-완전 문제다.
그래프 순회
그래프 순회란 그래프 탐색이라고도 불리우며 그래프의 각 정점을 방문하는 과정을 말한다.
그래프의 각 정점을 방문하는 그래프 순회에는 크게 깊이 우선 탐색(Depth-First Search, DFS)와 너비 우선 탐색(Breadth-First search, BFS)의 2가지 알고리즘이 있다. 일반적으로 DFS가 BFS보다 더 널리 쓰인다. DFS는 주로 스택으로 구현하며 백트래킹을 통해 뛰어난 효용을 보여주며, BFS는 큐로 구현하며 그래프의 최단 경로를 구하는 문제 등에 사용한다. 그래프를 표현하는 방법에는 크게 인접 행렬과 인접 리스트의 2가지 방법이 있는데 여기서는 인접 리스트로 표현하도록 한다.
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
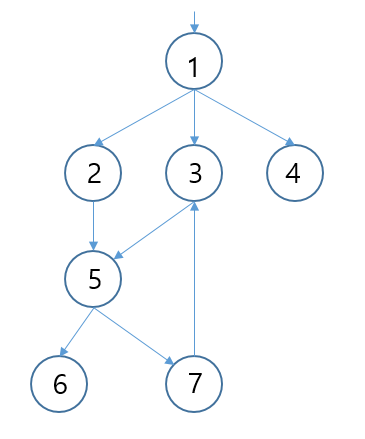
DFS
재귀 구조로 구현
def recursive_dfs(v, discovered=[]):
discovered.append(v)
for w in graph[v]:
if w not in discovered:
discovered = recursive_dfs(w, discovered)
return discovered
print(f'recursive dfs: {recursive_dfs(1)}')
out:
recursive dfs: [1, 2, 5, 6, 7, 3, 4]
return 된 값을 보면 그래프의 깊이 순에 따라서 조회하는 것을 확인할 수 있다.
스택을 이용한 반복 구조로 구현
def iterative_dfs(start_v):
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in graph[v]:
stack.append(w)
return discovered
print(f'iterative dfs: {iterative_dfs(1)}')
out:
iterative dfs: [1, 4, 3, 5, 7, 6, 2]
같은 DFS이지만, 순서만 다를 뿐이다.
BFS
BFS는 DFS보다 쓰임새는 적지만, 최단 경로를 찾는 다익스트라 알고리즘 등에 유용하게 쓰인다.
큐를 이용한 반복 구조로 구현
def iterative_bfs(start_v):
discovered = [start_v]
queue = [start_v]
while queue:
v = queue.pop(0)
for w in graph[v]:
if w not in discovered:
discovered.append(w)
queue.append(w)
return discovered
print(f'iterative bfs: {iterative_bfs(1)}')
out:
iterative bfs: [1, 2, 3, 4, 5, 6, 7]
BFS는 재귀 구현이 불가능하다.
백트래킹
백트래킹(Backtracking)은 해결책에 대한 후보를 구축해 나아가다 가능성이 없다고 판단되는 즉시 후보를 포기(백트랙)해 정답을 찾아가는 범용적인 알고리즘으로 제약 충족 문제(Constraint Satisfaction Problems)에 특히 유용하다.
백트래킹은 DFS보다 좀더 광의의 의미를 지닌다. 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 뜻하며, DFS는 백트래킹의 골격을 이루는 알고리즘이다. 백트래킹은 가보고 되돌아오고를 반복한다. 얼핏 보면 모든 경우를 다 확인하는 브루트 포스와 유사하지만, 백트래킹은 탐색 후 가능성이 없어 보이면 후보를 포기할 수 있어 보다 유동적이다. 후보를 포기하고 백트래킹하는 과정을 트리의 가지치기(Pruning)라고 하며 트리의 탐색 최적화 문제와 관련이 깊다.
제약 충족 문제(Constraint Satisfaction Problems, CSP)
제약 충족 문제란 수많은 제약 조건(Constraint)을 충족하는 상태(Status)를 찾아내는 수학 문제를 일컫는다.
백트레킹은 제약 충족 문제를 풀이하는데 필수적인 알고리즘이다. CSP는 인공지능이나 경영 과학 분야에서 심도있게 연구되고 있다. CSP의 대표적인 문제로는 스도쿠가 있다.
섬의 개수
1을 육지로, 0을 물로 가정한 2D 그리드 맵이 주어졌을 때, 섬의 개수를 계산해라.
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1
- 풀이: DFS로 그래프 탐색
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
def dfs(i, j):
# 더 이상 땅이 아닌 경우 종료
if i < 0 or i >= len(grid) or \
j < 0 or j >= len(grid[0]) or \
grid[i][j] != '1':
return
# 탐색 한 육지를 0으로 변경
grid[i][j] = 0
# 동서남북 & 재귀를 통해 인접한 육지 모두 0으로 변경
dfs(i + 1, j)
dfs(i - 1, j)
dfs(i, j + 1)
dfs(i, j - 1)
count = 0
# 행렬의 입력값인 grid의 행, 열 단위로 육지(1)인 곳을 찾아 진행하다
# 육지 발견 시 sefl.dfs() 호출
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == '1':
dfs(i, j)
# 모든 육지 탐색 후 카운트 1 증가
count += 1
return count
전화 번호 문자 조합
2에서 9까지 숫자가 주어졌을 때 전화 번호로 조합 가능한 모든 문자를 출력하라.

Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
- 풀이: 모든 조합 탐색
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
def dfs(index, path):
# 끝까지 탐색하면 함수 종료하고 백트래킹
if len(path) == len(digits):
result.append(path)
return
# 입력값 자릿수 단위 반복
for i in range(index, len(digits)):
# 숫자에 해당하는 모든 문자열 반복
for j in dic[digits[i]]:
dfs(i + 1, path + j)
# 예외 처리
if not digits:
return []
dic = {"2": "abc", "3": "def", "4": "ghi", "5": "jkl",
"6": "mno", "7": "pqrs", "8": "tuv", "9": "wxyz"}
result = []
dfs(0, "")
return result
순열
서로 다른 정수를 입력받아 가능한 모든 순열을 리턴하라.
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
- 풀이: DFS를 활용한 순열 생성
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
results = []
prev_elements = []
def dfs(elements):
# 리프 노드일때 결과 추가
if len(elements) == 0:
# [:]를 안하면 prev_element에 대한 참조값이 추가되어 참조값이 변경
results.append(prev_elements[:])
# 순열 생성 재귀 호출
for e in elements:
next_elements = elements[:]
next_elements.remove(e)
prev_elements.append(e)
dfs(next_elements)
prev_elements.pop()
dfs(nums)
return results
- itertools 모듈 사용
itertools 모듈은 반복자 생성에 최적화된 기능들을 제공하므로, 실무에서는 모듈 사용이 효율적이다.
import itertools
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
# itertools.permutations()는 튜플 형태로 반호나하기 때문에 list 처리 과정을 거침ㅁ
return list(itertools.permutations(nums))
조합
전체 수 n을 입력받아 k개의 조합을 리턴하라.
Input: n = 4, k = 2
Output: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Explanation: There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., [1,2] and [2,1] are considered to be the same combination.
- 풀이: DFS로 k개 조합 생성
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
results = []
def dfs(elements, start: int, k: int):
if k == 0:
results.append(elements[:])
return
# 자신 이전의 모든 값을 고정하여 재귀 호출
for i in range(start, n + 1):
elements.append(i)
dfs(elements, i + 1, k - 1)
elements.pop()
dfs([], 1, k)
return results
- itertools 모듈 사용
import itertools
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
return list(itertools.combinations(range(1, n + 1), k))
