Junhyuk Yu

I will be an amazing person.

해당 내용은 ‘파이썬 알고리즘 인터뷰’ 책의 일부를 발췌하여 정리한 내용입니다.

트리는 계층형 트리 구조를 시뮬레이션 하는 추상 자료형(ADT)으로, 루트 값과 부모-자식 관계의 서브트리로 구성되며, 서로 연결된 노드의 집합이다.

트리 구조는 위아래 개념을 컴퓨터에서 표현한 구조다. 트리의 중요 속성 중 하나는 재귀로 정의된(Recursively Defined) 자기 참조(Self-Referential) 자료구조라는 점이다.

트리의 각 명칭

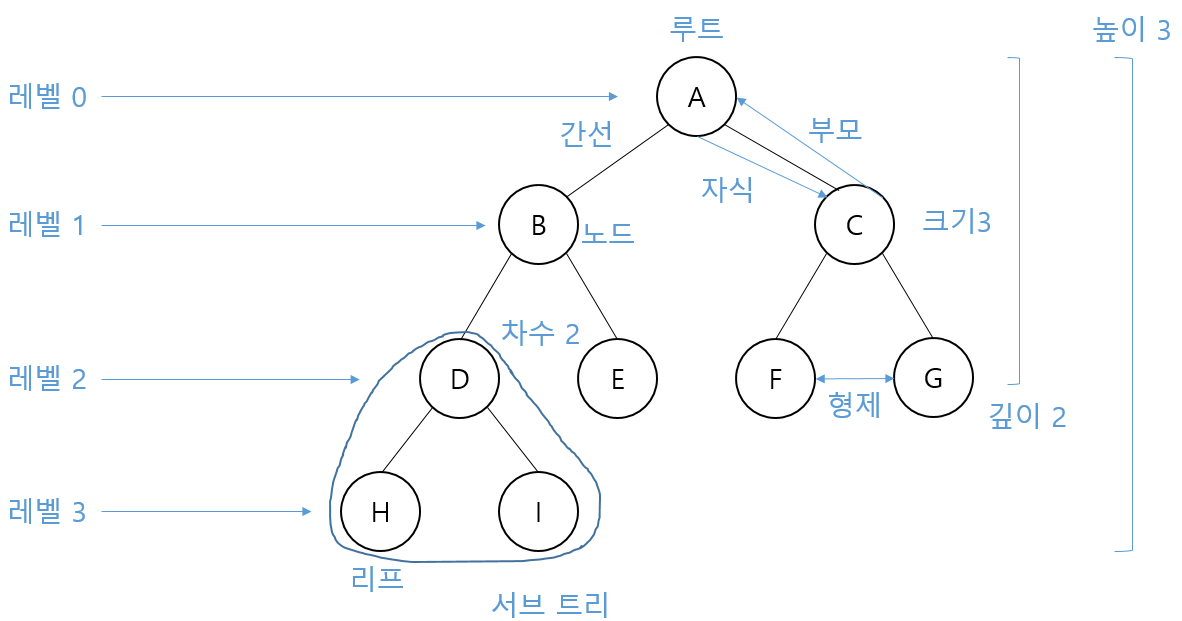
트리는 항상 루트(Root)에서부터 시작되며, 자식(Child) 노드를 가지고 간선(Edge)으로 연결되어 있다.

  • 차수(Degree): 자식 노드의 개수
  • 크기(Size): 자신을 포함한 모든 자식 노드의 개수
  • 높이(Height): 현재 위치에서 부터 리프(Leaf)까지의 거리
  • 깊이(Depth): 루트에서부터 현재 노드까지의 거리

트리는 항상 단방향이기 때문에 간선의 화살표는 생략 가능하다.

그래프 vs 트리

트리는 순환 구조를 갖지 않는 그래프이다.

핵심은 순호나구조가 아니라는 데 있다. 트리는 특수한 형태의 그래프의 일종이며 그래프의 범주에 포함된다. 하지만, 트리는 그래프와 달리 한번 연결된 노드가 다시 연결되는 법이 없다. 그뿐만 아니라 트리는 하나의 부모 노드를 갖는다는 차이점이 있으며 루트 또한 하나이다.

이진 트리

이진 트리는 왼쪽, 오른쪽, 최대 2개의 자식을 갖는 매우 단순한 형태로, 다진 트리에 비해 훨씬 간결할 뿐만 아니라 여러 가지 알고리즘을 구현하는 일도 좀 더 간단히 처리할 수 있어 대체로 특별한 경우가 아니면 트리는 이진 트리를 일컫는다.

이진 트리의 최대 깊이

이진 트리의 최대 깊이를 구하라.

Input: root = [3,9,20,null,null,15,7]
Output: 3
  • 풀이: 반복 구조로 BFS 풀이

리스트 형태로 풀이해도 되지만, 양방향 추출이 많은 경우 deque를 사용하면 속도를 향상시킬 수 있다.

import collections

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        queue = collections.deque([root])
        depth = 0

        while queue:
            depth += 1
            # 큐 연산 추출 노드의 자식 노드 삽입
            for _ in range(len(queue)):
                cur_root = queue.popleft()
                if cur_root.left:
                    queue.append(cur_root.left)
                if cur_root.right:
                    queue.append(cur_root.right)
        # BFS 반복 횟수 == 깊이
        return depth

⚠️root: TreeNode를 통해서 root의 입력값이 트리 형태로 묶여서 maxDepth에 들어간다. 만약, 그냥 root가 queue에 담기게 된다면, queue.popleft()를 할 경우, 초기 root값이 그대로 나오고 queue는 []만 존재하게 된다는 것을 유의하자.

이진 트리의 직경

이진 트리에서 두 노드 간 가장 긴 경로의 길이를 출력하라.

Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
  • 풀이: 상태값 누적 트리 DFS
# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    longest: int = 0

    def diameterOfBinaryTree(self, root: TreeNode) -> int:
        def dfs(node: TreeNode) -> int:
            if not node:
                return -1
            # 왼쪽, 오른쪽 각각 리프 노드까지 탐색
            left = dfs(node.left)
            right = dfs(node.right)

            # 가장 긴 경로
            self.longest = max(self.longest, left + right + 2)
            # 상태값
            return max(left, right) + 1

        dfs(root)
        return self.longest

⚠️dfs를 마쳤을 때 반환하는 값은 max(left, right) + 1이다. 이 코드에서는 DFS를 통해서 트리 최 하단까지 탐색을 진행한 후, 가장 최하단의 left와 right값이 -1이 된다. 즉, 가장 하단에서 return해주는 값은 1이 된다. left와 right는 그 해당 노드의 값이 아니라는 것을 유념해두자.

You may also enjoy