비선형 자료구조 - 트리 lll
해당 내용은 ‘파이썬 알고리즘 인터뷰’ 책의 일부를 발췌하여 정리한 내용입니다.
이진 탐색 트리(BST)
이진 탐색 트리란 정렬된 트리를 의미한다. 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드로 구성되어 있고 오른쪽 서브트리는 노드의 값과 같거나 큰 값들을 지닌 노드들로 이루어져있는 트리를 뜻한다. 이 트리의 최고 장점이라 하면 탐색 시 시간 복잡도가 O(logn)이라는 점이다.
하지만 운이 나쁘게도 트리의 연결순서가 1-2-3-4-5-6-7로 이루어져있다면 연결리스트나 다름없어진다. 7을 찾으려면 7번의 연산을 수행해야한다는 뜻이다. 만약, 연결리스트 형태로 이루어진 트리가 100만번까지 이어진다면 어마어마한 연산을 수행해야 한다. 이를 해결 하기 위해서 고안한 방법이 ‘자가 균형 이진 탐색 트리’다.
자가 균형 이진 탐색 트리
자가 균형(또는 높이 균형) 이진 탐색 트리는 삽입, 삭제 시 자동으로 높이를 작게 유지하는 노드 기반의 이진 탐색 트리다.
자가 균형 이진 탐색트리의 대표적인 형태로는 AVL트리와 레드-블랙 트리 등이 있으며, 레드-블랙 트리는 실무에서 매우 빈번히 쓰이는 트리 형태이다.
정렬된 배열의 이진 탐색 트리 변환
오름차순으로 정렬도니 배열을 높이 균형 이진 탐색트리로 변환하라.
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
- 풀이: 이진 검색 결과로 트리 구성
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if not nums:
return None
mid = len(nums) // 2
node = TreeNode(nums[mid])
node.left = self.sortedArrayToBST(nums[:mid])
node.right = self.sortedArrayToBST(nums[mid + 1:])
return node
이진 탐색 트리를 더 큰 수 합계 트리로
BST의 각 노드를 현재값보다 더 큰 값을 가진 모든 노드의 합으로 만들어라.
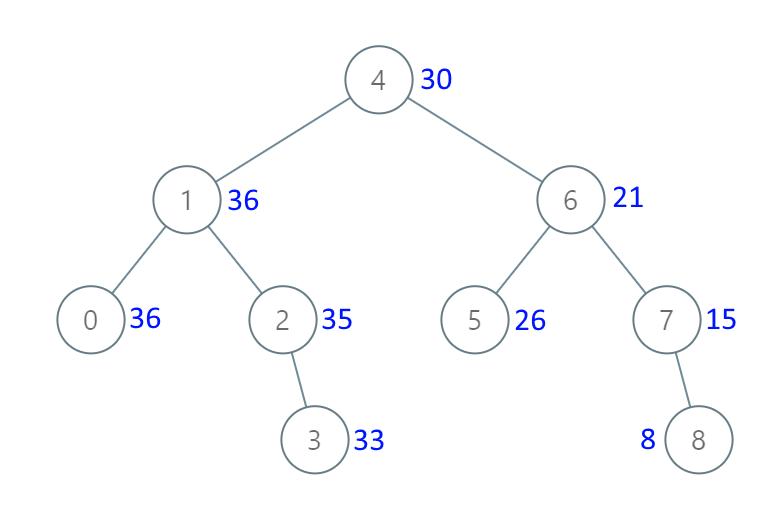
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
- 풀이: 중위 순회로 노드 값 누적
# Definition for a binary tree node.
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
val: int = 0
def bstToGst(self, root: TreeNode) -> TreeNode:
# 중위 순회 노드 값 누적
if root:
self.bstToGst(root.right)
# self.val: 지금까지 누적된 값
# root.val: 현재 노드의 값
self.val += root.val
root.val = self.val
self.bstToGst(root.left)
return root
이진 탐색 트리 합의 범위
이진 탐색 트리가 주어졌을 때 L이상 R이하의 값을 지닌 노드의 합을 구하라.
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
- 풀이: DFS + 가지치기
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: TreeNode, L: int, R: int) -> int:
def dfs(node: TreeNode):
if not node:
return 0
if node.val < L:
return dfs(node.right)
elif node.val > R:
return dfs(node.left)
return node.val + dfs(node.left) + dfs(node.right)
return dfs(root)
이진 탐색 트리 노드 간 최소거리
두 노드 간 값의 차이가 가장 작은 노드의 값의 차이를 출력하라.
Input: root = [4,2,6,1,3]
Output: 1
기본적으로 이진 탐색 트리는 왼쪽보다 오른쪽의 값이 크다. 그렇다는 뜻은 뻗어나간 트리의 가지에서 가장 오른쪽끼리의 차이가 제일 적다. 물론, 최상단의 루트와 그 다음 노드값이 최소가 될 수 있기에 마지막에 이를 비교하는 코드를 작성하면 된다.
- 풀이: 재귀 구조로 중위 순회
class Solution:
# 시스템 내 최소값과 최대값 설정
prev = -sys.maxsize
result = sys.maxsize
# 재귀 구조 중위 순회 비교 결과
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
if root.left:
self.minDiffInBST(root.left)
self.result = min(self.result, root.val - self.prev)
self.prev = root.val
if root.right:
self.minDiffInBST(root.right)
return self.result
- 풀이: 반복 구조로 중위 순회
class Solution:
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
prev = -sys.maxsize
result = sys.maxsize
stack = []
node = root
while stack or node:
while node:
stack.append(node)
node = node.left
node = stack.pop()
result = min(result, node.val - prev)
prev = node.val
node = node.right
return result
트리 순회
트리 순회란 그래프 순회의 한 형태로 트리 자료구조에서 각 노드를 정확히 한번 방문하는 과정을 말한다.
트리 순회에는 크게 현재 노드를 먼저 순회한 후 왼쪽과 오른쪽 서브트리를 순회하는 전위순회, 왼쪽 서브트리를 순화한 다음 현재 노드를 순회하는 중위순회, 그리고 왼쪽과 오른쪽 서브트리를 순회한 다음 현재 노드를 순회하는 후위 순회로 나뉘어진다.
전위, 중위 순회 결과로 이진 트리 구축
트리의 전위, 중위 순회 결과를 입력값으로 받아 이진 트리를 구축하라.
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
- 풀이: 전위 순회 결과로 중위 순회 분할 정복
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if inorder:
# 전위 순회 결과는 중위 순회 분할 인덱스
index = inorder.index(preorder.pop(0))
# 중위 순회 결과 분할 정복
node = TreeNode(inorder[index])
node.left = self.buildTree(preorder, inorder[0:index])
node.right = self.buildTree(preorder, inorder[index + 1:])
return node
