실습으로 배우는 머신러닝 교육과정 II
⚠️ 해당 내용은 K-MOOC의 실습으로 배우는 머신러닝 교육과정의 일부를 정리한 내용입니다.
Logistic regression
Logistic Regression의 필요성
Logistic Regression의 목적
- 이진형(0,1)의 형태를 갖는 종속변수(분류문제)에 대해 회귀식으로 형태로 모형을 추정하는 것
왜 회귀식으로 표현해야하는가?
- 회귀식으로 표현될 경우 변수의 통계적 유의성 분석 및 종속변수에 미치는 영향력 등을 알 수 있음
Logistic Regression의 특정
- 이진형 종속변수 Y에 대한 로짓함수(logit function)를 회귀식의 종속변수로 사용
- 로짓함수는 설명 변수의 선형결합으로 표현됨
- 로짓함수의 값은 종속변수에 대한 성공확률로 역산될 수 있으며 따라서 이는 분류 문제에 적용 가능함
예제
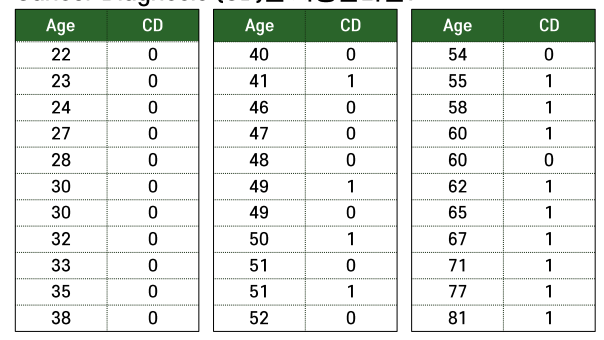
- 2진형 변수를 그대로 사용하면 회귀에서 우리가 원하는 함수를 도출하기 어려움
- 따라서 나이 그룹을 만들고 그 안에 몇퍼센트로 존재하는지로 바꿔줌.
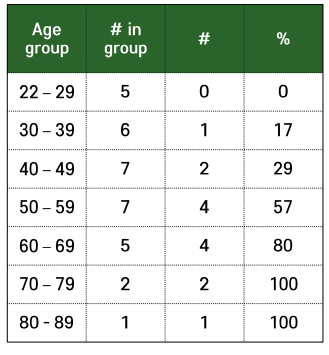
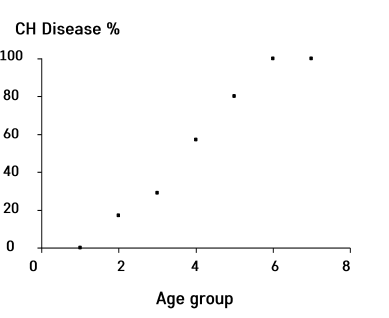
- 이런 식으로 변환하면 우리가 원하는 함수를 구할 수 있는 형태로 만들 수 있음.
sigmoid function
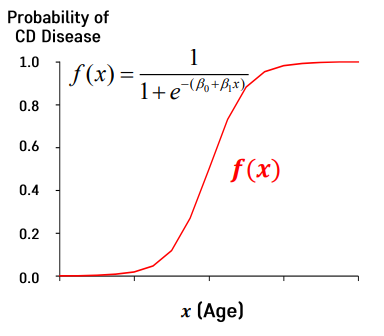
- Sigmoid 함수는 x가 0일때 y가 0.5가 되는 값.
- 만약, x가 음수로 갈 수록 분모가 무한대로 커지면서 y값이 0에 수렴
- 반대로 x가 양의 수로 갈수록 분모는 1에 수렴하게 되면서 y값이 0에 수렴
Cross-Entropy
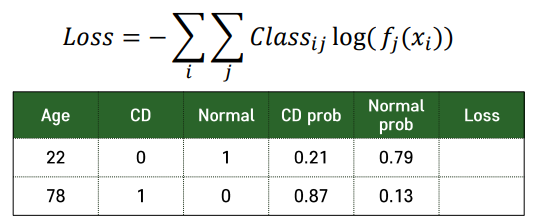
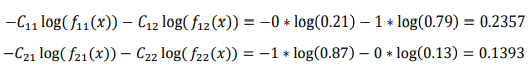
- i = 관측치의 index, j = 클래스의 index
- CD, Normal ⇒ 클래스, CD prob, Norman prob ⇒ function
최적화와 모형 학습
Machine Learning and Optimiaztion
- Loss를 최소화함으로써 머신러닝 모델들을 최적화
Linear Regression
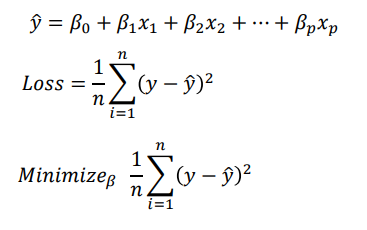
- y_hat = liniear regression에서 예상한 함수와 그 함수의 y값
- 집중적으로 다룰 파트가 Minimize B 항목 ⇒ Optimizaiton
Loss Function of Neural Networks
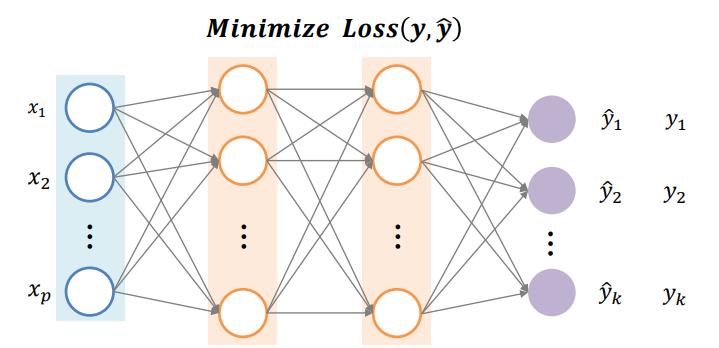
- 선 하나가 parameter
- 최신 모델들은 수만게의 parameter를 사용하고 있음
- 손으로 plot을 하기 어려움(굉장히 고차원적임).
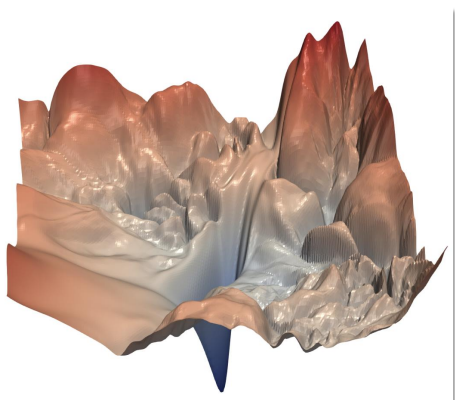
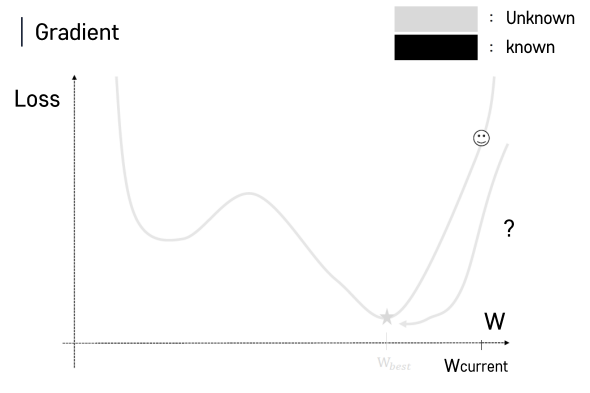
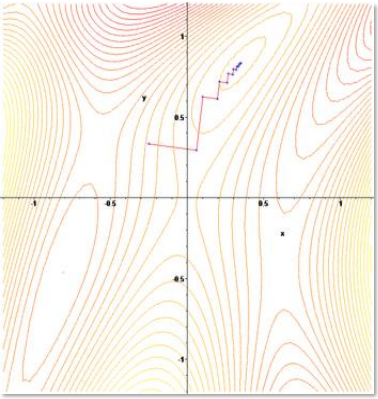
경사하강법 개요
Gradient(기울기) Descent
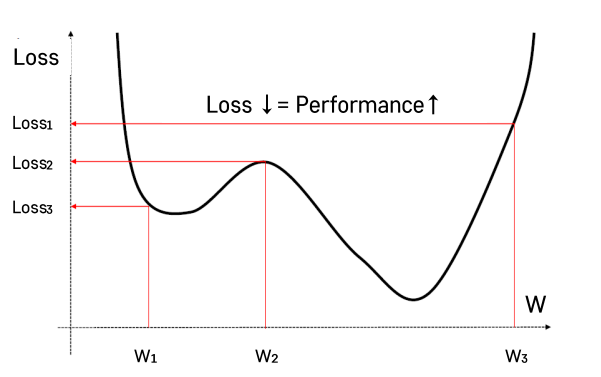
- Gardient를 이용해서 함수값을 줄인다.
- 러닝머신에서는 Loss를 줄여야 최고의 퍼포먼스를 낼 수 있음.
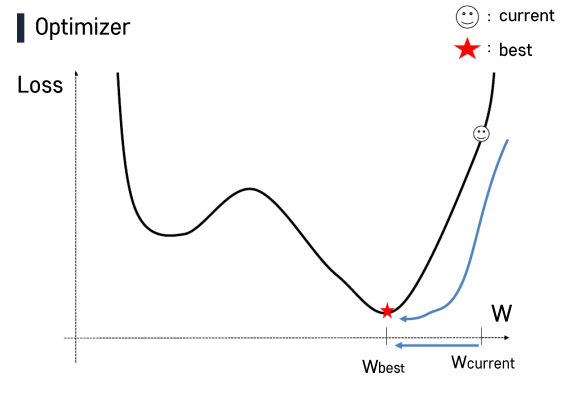
- y = wx
- 초기 w는 랜덤하게 설정.
- w값에서 loss가 최소인 값으로 점점 이동하게됨.
- 하지만 수천, 수만개의 w값이 있는 그래프에선 찾기가 매우 어려워짐.
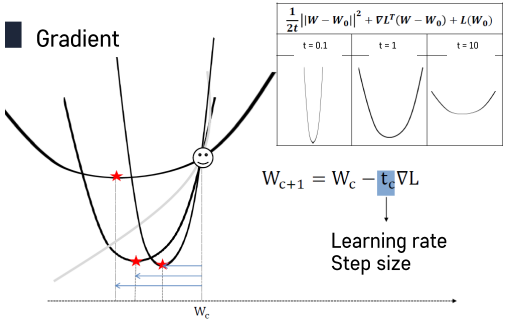
- 테일러 급수 전개를 제시하면서 Quadratic(2차 다항식) approximiation 방법을 사용.
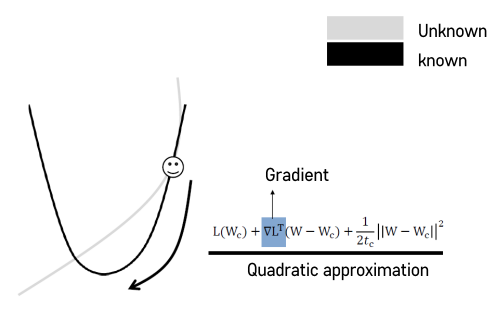
- L(Wc) : 현재 위치에서의 W값.
- Wc : Constant, W : Variable
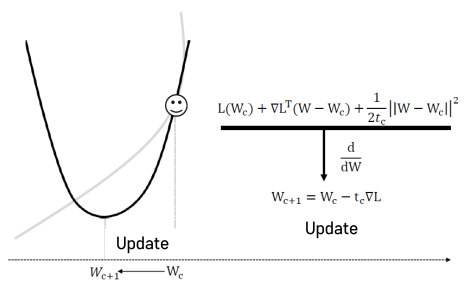
- Wc+1 : Wc의 한번 업데이트 된 상황.
- tc : Step Size. 사람이 결정하는 숫자. 중요한 Hyperparameter
- 우리가 실제 함수값을 모르기 때문에 approximation해서 최소값을 구하는 과정
경사하강법 심화
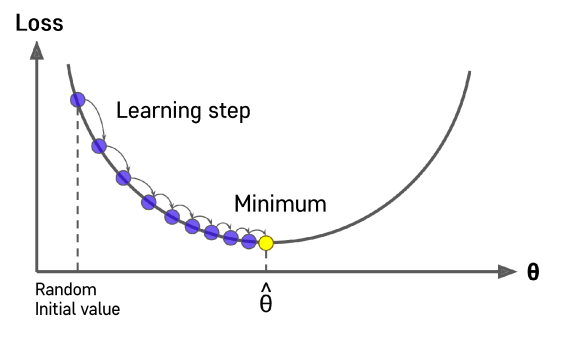
Learning Rate
- Step size(tc)의 크기에 따라 예측되는 그래프의 사이즈가 달라짐. Learning Rate라고 부르기도 함
-
이상적인 learning rate
-
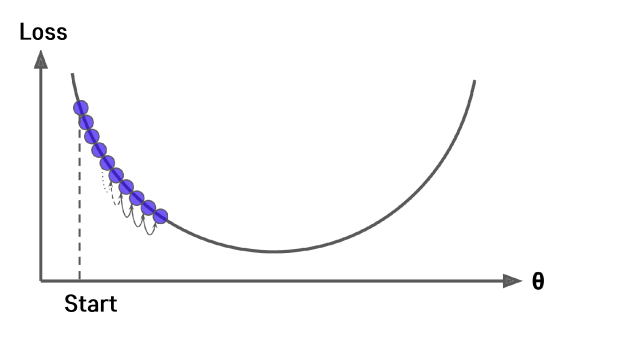
너무 작은 learning rate.
- 지금은 2차원 형태라 심플하지만, 고차원의 큰 함수의 경우 잘못 설정하면 월 단위로 끝나는 데이터를 몇배로 더 늘려버릴 수 있음.
- 이런 상황을 보안하기 위해 Gradient Descent Optimizer를 사용
- Learnig rate를 상황에 맞게끔 적절하게 수정
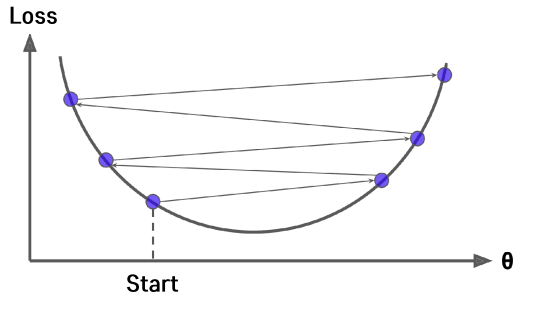
- 너무 큰 Learning Rate
Stochastic Gradient Descent
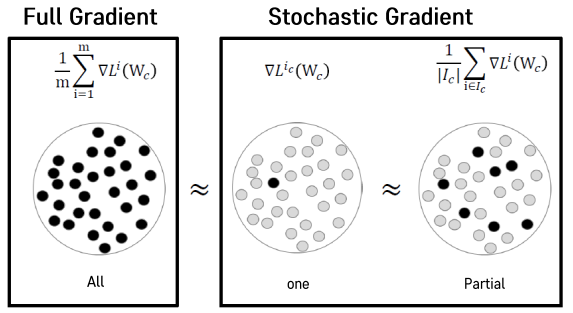
- 처리 과정에서 컴퓨팅적인 한계를 극복하기 위해, 데이터를 여러 조각(batch)으로 나눠주고 조각마다의 Gradient Descent를 계산해서 업데이트를 하는 방식.
- Deep Learning에서 많이 사용하는 방식
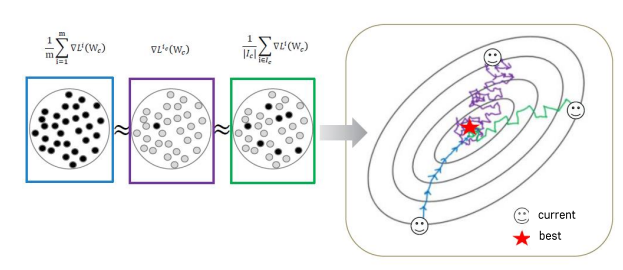
- SGD는 빠르게 해를 구할 수 있다는 장점을 가지고 있다.
- 기본적으로 데이터들을 일부 추출해서 GD를 해주는 방법을 추천
Momentum
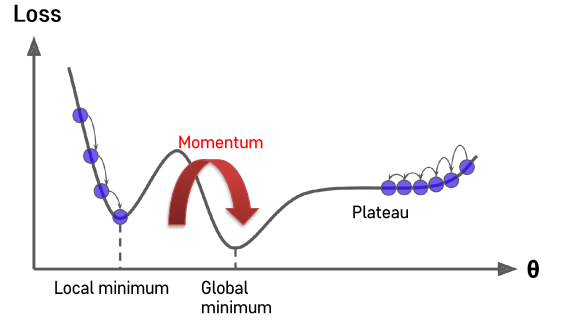
- Local minimum에서 GD가 끝나게 되면, Global Minumum을 찾지 못해 모델이 좋은 성능을 낼 수 없다.
- 이러한 Local minimun을 벗어나기 위해 Momentum이라는 기술을 활용.
- SGD + Momentum이 가장 딥러닝에서 널리 사용되는 기법
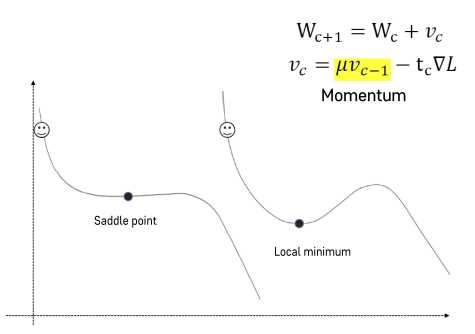
- 경사하강하면서 내려온 속도를 기억해주어 그 값만큼 더해주는 것이 Momentum
- Momentum을 더해줌으로써 Saddle point 또는 local minimum을 벗어나 더 작은 minimum point를 찾을 수 있음.
Support Vector Machine
Support Vector Machine
- 선형이나 비선형, 분류, 회귀, 이상치 탐색에도 사용할 수 있는 머신러닝 방법론
- 딥러닝 이전 시대까지 널리 사용되던 방법론
- 복잡한 분류문제를 잘 해결, 상대적으로 작거나 중간크기의 가진 데이터에 적합
- 방대한 양에서는 딥러닝이 유용
- 최적화 모형으로 모델링 후 최적의 분류 경계 탐색
- 딥러닝이 아직까지는 완벽한 알고리즘이 아님.
-
딥러닝이 커버 못하는 영역들을 다른 알고리즘들이 커버
-
- 알고리즘마다의 장단점을 잘 활용해서 상황에 따라 잘 적용하는 것이 중요.
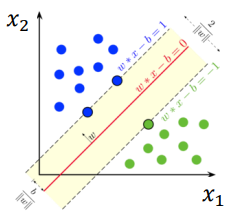
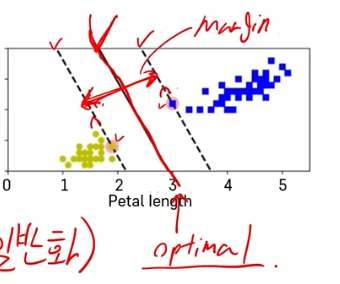
- Large margin classification : 두 클래스 사이에 가장 넓이가 큰 분류 경계선을 찾음
- 가운데 optimal선과 가상의 점선 사이를 ‘margin’이라고 함. 데이터 값들은 이 margin을 넘어설 수 없음.
- Support Vector : 각각의 클래스에서 분류 경계선을 지지하는 관측치
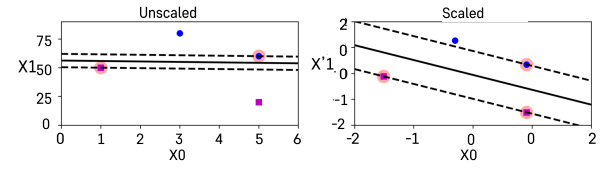
- SVM은 스케일에 민감하기 때문에 변수들 간의 스케일을 잘 맞춰주는 것이 중요
- Sklearn의
StandardScaler()를 사용하면 스케일을 잘 맞출 수 있음
- Sklearn의
Hard Margin vs Soft Margin
- Hard Margin : 두 클래스가 하나의 선으로 완벽하게 나눠지는 경우
-
Hard margin을 충족하는 데이터 셋은 많이 없음.
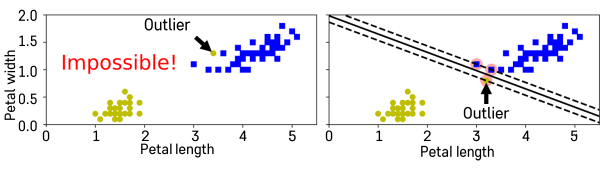
-
- Soft Margin : 일부 샘플들이 분류경계선의 분류 겨로가에 반하는 경우를 일정 수준 허용하는 방법
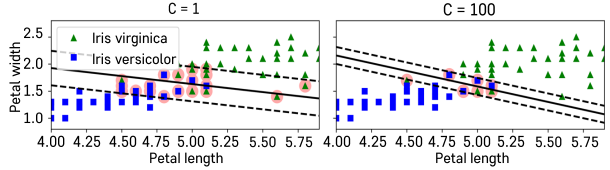
- C 패널티 파라미터로 조정(SVM-Hyperparameter)
- c값을 작게 주면 Margin이 넓어지지만, 오차도 커지게 됨
- c값을 크게 주면 오차가 줄지만, Margin도 좁아지게 됨
- C 패널티 파라미터로 조정(SVM-Hyperparameter)
Hard Margin Optimization
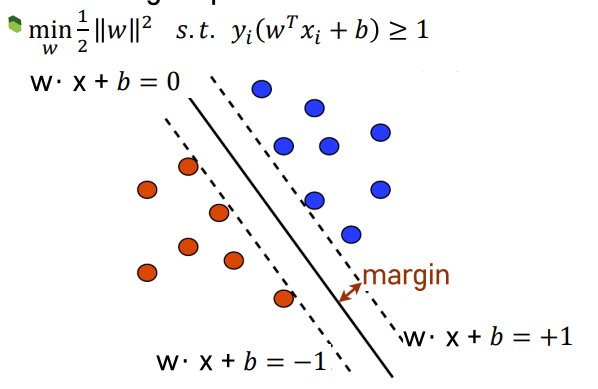
-
목적식. Margin을 최대화할 때 성능이 좋아짐. w벡터의 값을 최대화 할 때 값이 커짐.
\[min*1/2*||w||^2\] - W*x + b = 0 ⇒ 분류경계선(평면의 방정식)
- yi : 특정 관측치들에 대한 클래스 부여. 지금 예시의 경우, 붉은 색은 -1, 파란색은 +1로 클래스를 부여함
- W*x + b = +1 or -1
Margin 계산
-
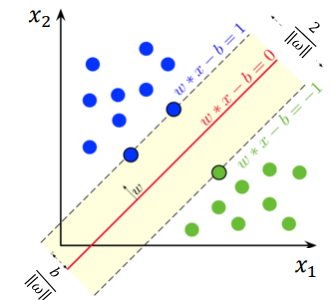
임의의 점 x’ = (x0,x1)에서 평면 wx + b -1 = 0까지의 거리
$ wx’ + b - 1 / w $ -
평면 wx + b = 0 위의 점 x’’ = (x0, x1)에서 평면 wx + b -1 = 0까지의 거리
\[|wx'' + b - 1|/||w|| = 1/||w||\] -
wx + b + 1 = 0 평면까지의 거리까지 고려하면 margin의 길이는 2/ w -
Margin 길이를 최대화 ⇒ 1/2 w ^2 최소화
Soft margin Optimizaiton

- ξi : 관측치들에 대한 오차
- C : 페널티 파라미터
SVM Prediction
Nonlinear SVM
Nonliniear SVM Classification
- 기본적인 아이디어 : 다항식 변수들을 추가함으로써 직선으로 분류할 수 있는 형태로 데이터 만들기
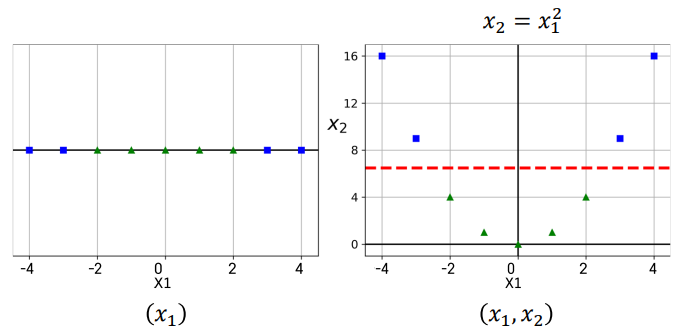
- 1차원형의 데이터는 SVM 라인을 그려줄수가 없음. 그래서 새로운 변수를 만들어서 라인을 그려주게 됨.
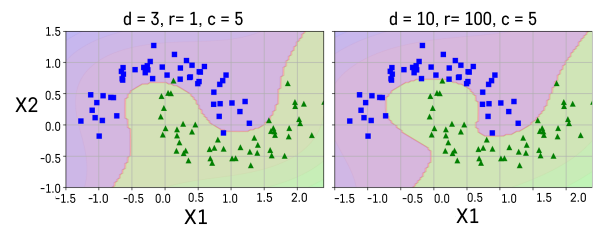
- Polynomial Kernel : 다항식 차수를 조절할 수 있는 효율적인 계산 방법
- Gaussian RBF(Radial Basis Function) Kernel : 무한대 차수를 갖는 다항식을 차원으로 확장시켜주는 효과
- gamma - 고차항 차수에 대한 가중 정도
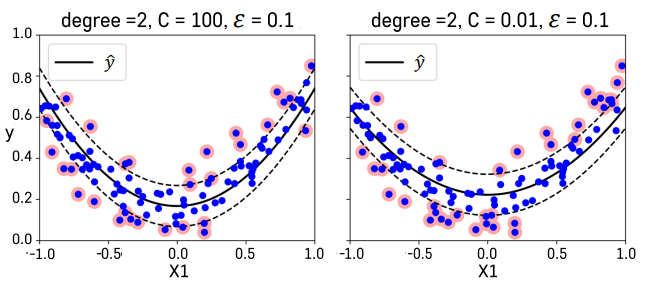
SVM Regression
- 선형회귀식을 중심으로 이와 평행한 오차 한계선을 가정하고 오차한계선 너비가 최대가 되면서 오차한계선을 넘어가는 관측치들에 페널티를 부여하는 방식으로 선형 회귀식 추정
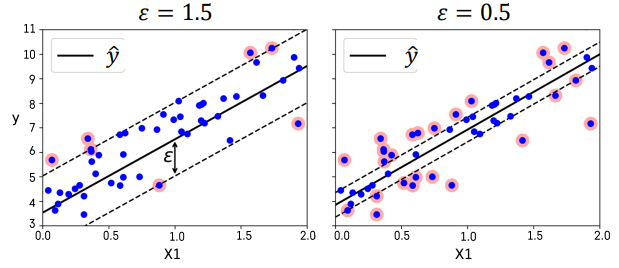
- 다항식 변수항을 추가하는 개념을 도입함으로써 비선형적인 회귀 모형을 적합할 수 있다.