실습으로 배우는 머신러닝 교육과정 I

⚠️ 해당 내용은 K-MOOC의 실습으로 배우는 머신러닝 교육과정의 일부를 정리한 내용입니다.

인공지능과 머신러닝의 개념

머신러닝은 인공지능의 하위 개념.

머신러닝은 함수를 학습하는 것.

• 과거의 AI : Knowledge Engineering

컴퓨터가 학습하는 함수를 사람이 직접 코딩

• 현재의 AI : Machine Learning

컴퓨터 스스로 함수를 학습.

AI & Machine Learning & Deep Learning

• 딥러닝은 머신러닝의 일종. 하위 알고리즘.
• 인공지능은 굉장히 광범위한 개념
  • 머신러닝 : 인공지능의 하위 개념
  • 빅데이터에로 학습하는데 굉장히 유리
    • 딥러닝 : 머신러닝의 하위 개념.
    • 인지능력, 오감과 관련된 모델링을 하는데 가장 좋은 성능
    • 딥러닝이 각광받는 이유
      • 사람의 인지능력, 지적능력을 모사하는데 좋은 성능

Why Machine Learning?

• 우리는 빅데이터(1초에 약 1000TB가 발생)의 시대에 살고 있다.
• 머신러닝은 빅데이터를 이용해서 유용한 함수를 학습하는 방법
• 머신러닝의 좋은 자양분이 되어짐
• 이러한 현상이 굉장히 광범위하고 전지구적인 현상

머신러닝의 실현 가능성

• 많은양의 데이터를 처리하는 능력 → 하드웨어적인 능력
• 분산화된 컴퓨팅이 가능한 장비가 등장하여 머신러닝이 더 쉬워짐
• 최근에는 GPU(그래픽카드)를 이용해서 컴퓨팅을 진행
  • 빠르게 쉬운 계산들을 분산해서 처리할 수 있는것이 큰 장점.
  • 딥러닝의이 발전을 가속화하는데 큰 역할을 함.

CPU Computing vs GPU Computing

• CPU : 하나의 연산을 한번에 하나씩 처리
• GPU : 여러게의 연산을 여러번에 나눠서 한번에 처리
• IT 기업들이 머신러닝 기술들을 이용하여 새로운 패턴을 찾고 기존에 없던 새로운 가치를 만들어내고 있다.

머신러닝의 정의

컴퓨터 프로그램이 스스로 학습하게 하는 컴퓨팅 알고리즘을 뜻함

• Environment(E)
  • 러닝 시스템에 경험(데이터)들을 바탕으로 학습. 추상적 표현으로는 환경을 제공.
• Data(D)
  • 활동의 저장 결과
• Model(M)
  • 함수
• Performance(P)
  • 함수에 대한 평가

Model Evaluation and Performance

input과 output간의 상관관계를 적절하게 설명할 수 있는 함수를 찾아야함.

오차가 작은것이 좋음

• Mean Squared Error

머신러닝 학습 개념

Linear Regression

• 기본적인 머신 러닝
• 통계적으로도 사용

• 선형적인 관계를 기반으로 모형을 만듦.

  

  

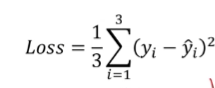
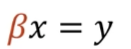
• x값과 y값만을 이용해서 Linear Regression 방법(수식)을 통해 loss함수를 정의하고, 함수(베타값)을 구하는 것이 목표.

머신러닝 프로세스 및 활용

Category of Machine Learning

• Machine Learning
  • Supervised Learning : 강의 대부분을 여기에 할애할 예정
  • Unsupervised Learning : 비지도 학습
    • Clustering
  • Rainfocement Learning(강화학습)

Supervised Learning

• 결과물(y)가 범주형이다 : Classification(분류)
• 결과물(y)가 연속적이다 : Regression(회귀)

Regression Example

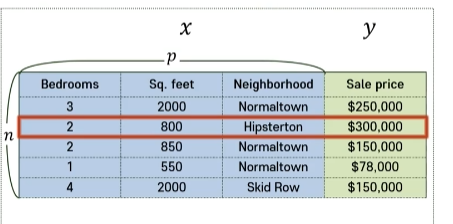
x : 입력변수, y : 출력변수, n : 관측치의 개수, p : 변수의 개수

Classification Example

x : 테이블 형태의 input, y : 범주형 변수, n : 이미지 하나

Model Evaluation and Performance

• ‘적절한 함수’를 학습시키는 것이 중요.

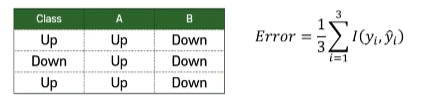
• 오차가 적은 모델이 더 적합 ⇒ A모델이 적합한 모델.

Machine Learning and Optimization

• 큰 틀에서 보면 minimize loss function 절차
• Huristic : 대략적인 알고리즘적인 접근을 통해 손실함수가 최소화되게 끔 유도
• 관통하는 기본 개념 : loss function을 정의하고 실제 모형이 출력하는 값하고의 차이를 최소화하게 함.

Generalization Error and Hyperparameter

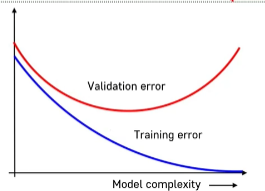
• 대부분의 케이스에서는 우리는 내가 가지지 않은 데이터를 뎅치터 내에서 잘 예측하기를 원한다.
• Training error : 내가 학습시키는 그 데이터 내에서 발생하는 오차
• Validation error : validation 데이터에 있는 실제 y랑 모형에서 출력된 y랑 정말 차이가 큰지 작은지 검증용으로 쓰는 에러
• 모형이 복잡해지거나 단순해지는 것에 대한 정의
  • 모형(함수)을 분류하는 패턴의 변동폭과 디테일하게 경계선을 만들어내냐의 차이
• Validation error가 최소가 되는 포인트를 찾아서 적절한 모형을 찾아야한다.
• hyperparameter : model의 complexity를 결정하는데 영향을 줌

Model Validatiuon with Data

• Training data만 사용하는 법 ⇒ 일반화가 잘 안되기 때문에 결과가 좋지 않음
• Train & Test Data로 나누기 ⇒ 튜닝이 된 다음에 사용할 수 있는 방법
• raining, Validation, Testing data로 나누기 ⇒ 가장 권장하는 방법.
  • train 데이터로 데이터를 학습시키고 그 다음에 학습된 결과를 validation 데이터에 적용
  • hyperparameter들을 적용해보면서 validation을 해보고 가장 좋은 hyperparameter를 찾기
  • 가장 적합한 hyperparamter를 적용해서 학습한 모형을 갖고 최종적으로 테스트 진행
• Cross-Validation : 데이터가 적을 때 사용할 수 있는 방법.

머신러닝 프로세스 개요

Data Science Process

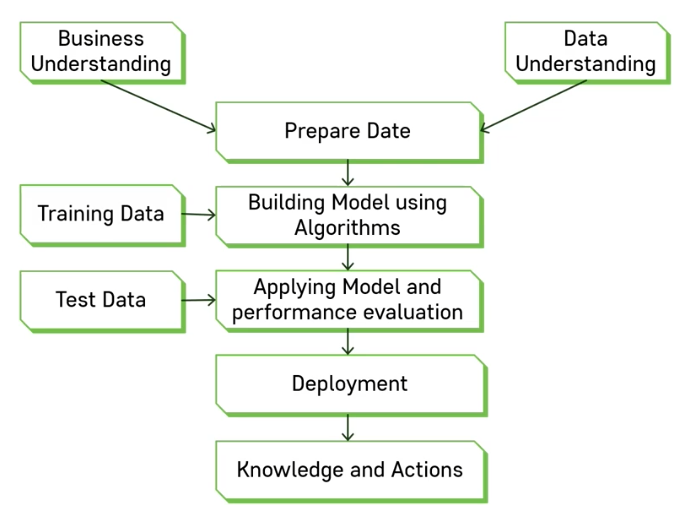
• Business Understainding : 본인이 해결하고자 하는 문제에 대한 정확한 이해.
• Data Understainding : 데이터의 구체적인 이해.

Deployment : 현실의 문제에 적용할 때 문제가 생길 수 있는 부분.

Data 관련 용어

• Dataset : 정의된 구조로 모야져있는 데이터 집합
• Data Point(Obersvation) : 데이터 세트에 속해있는 하나의 관측치
• Feature (Variable, Attribute) : 데이터를 구성하는 하나의 특성(숫자형, 범주형, 시간, 텍스트, 이진형)
• Label(Target, Response) : 입력 변수들에 의해 예측, 분류되는 출력 변수

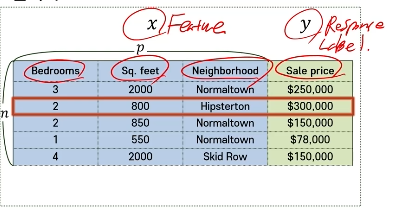
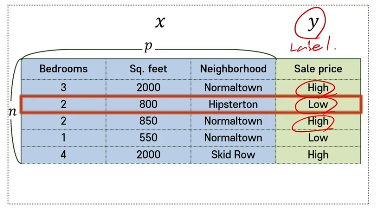
분류와 회귀

	분류	회귀
결과	종속변수(y)가 범주형일 때 사용하는 모델	종속변수가 연속형일때 사용하는 모델

데이터 준비과정

• Dataset Exploration : 데이터 변수 별 기본적인 특성들을 탐색하고 데이터의 분포적인 특징을 이해
• Missing Value : 결측치가 있는 경우 보정 필요
• Data Types an Conversion : 여러 종류의 데이터 타입이 있을 수 있기에 분석가능한 형태로 변환후 사용해야 함
• Normalization : 변수들이 다른 경우 모델 학습에 영향을 주기 때문에 정규화 과정을 거침
• Outliers : 다른 관측치와 크게 차이나는 관측치들이 존재. 이 관척치들들 모델링 전 처리가 필요함.
• Feature Selection : 변수들 중에서 중요한 변수가 있고 그렇지 않은 변수들이 있음. 선택이 필요한 경우가 존재.
• Data Sampling : 모델을 검증 or 이상 관측치 탐색 or 앙상블 모델리을 할 떄 가지고 있는 데이터를 일부분 추출하는 과정을 거치기도 함.

Modeling

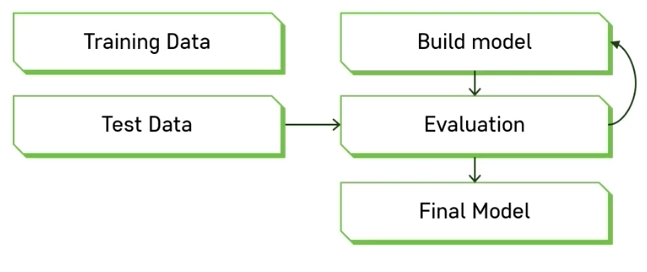
• Model : 입력변수와 출력변수간의 관계를 정의해줄 수 있는 추상적인 함수 구조

Modeling 검증

• Underfit : 너무 적은 데이터 학습
• Overfit : 너무 모양이 복잡해서 과적합

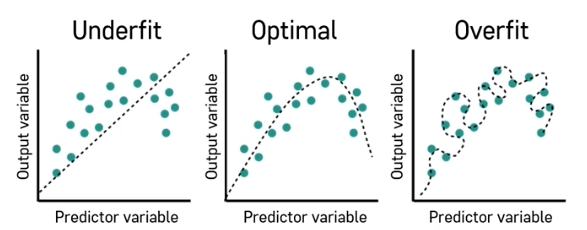
머신러닝 분류 모델링

Bias-Variance Tradeoff

참고 사이트

• 모든 모델은 복잡도를 통제할 수 있는 hyperparameter를 갖고 있음
• 가장 좋은 성능을 낼 수 있는 모델을 학습하기 위해 최적의 Hyperparanmeter를 결정해야함.
• 모형의 오차 = Bias + Variance
  • Bias : 예측값과 실제 정답과의 차이의 평균
  • Variance : 다양한 데이터 셋에 대하여 예측값이 얼만큼 변화할 수 있는지에 대한 양의 개념. flexibilit를 가지는지에 대한 의미로도 사용. 얼만큼 예측값이 퍼져서 다양하게 출력될 수 있는 정도
  • 가장 이상적인 Bias-Variance Tradeoff ⇒ Low Bias & Low Variance

  

  

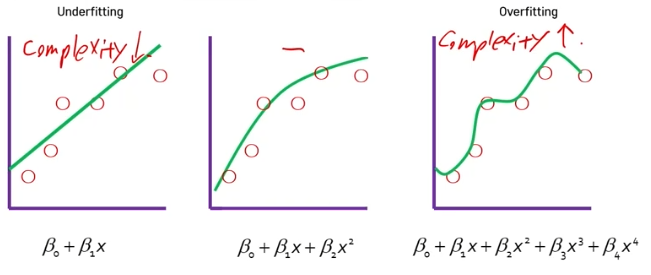
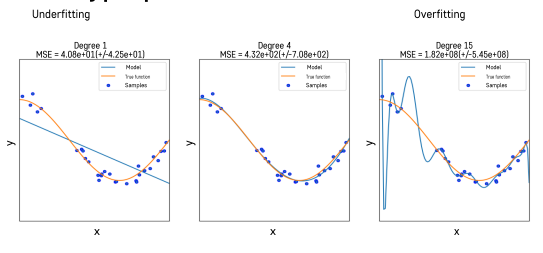
• 위 그래프를 보면 MSE의 경우 Overfitting이 중간 MSE보다 낮은 값을 보이고 있음
• 하지만 Training 오차를 측정한 값이고, plot을 보면 Complexity가 높은 모습을 확인할 수 있음. 변동성이 높은 경우 나타나는 현상

KNN

K-Nearest Neighbors

• K : 임의의 숫자
• “두 관측치의 거리(Target/Label)가 가까우면 Y도 비슷하다”
• K 개의 주변 관측치의 class 에 대한 majority voting(다수결의)
• Distance-based(거리에 기반) model, instance-based learning

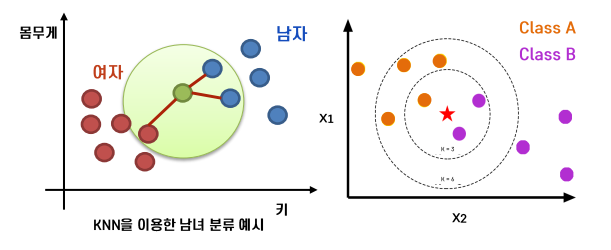
• 초록색 관측치가 여자일까 남자일까를 판단하기
  • k = 3으로 설정되어있음. 거리가 가장 가까운 관측치 3개를 선정.
  • 가장 가까운 3개의 후보군 중 남자 2명, 여자는 1명
  • 다수결의 시스템에 의해 초록색은 남자로 판별
• 붉은 색 별의 class 확인하기
  • k = 3일 때, 가까운 후보군 3개 선정하며, Class B가 A보다 많으므로 B로 선정
  • 반면, k가 6일 경우, A가 B보다 많으므로 A로 선정됨

⚠️ K의 값에 따라 판별되는 값이 달리질 수 있음.

거리

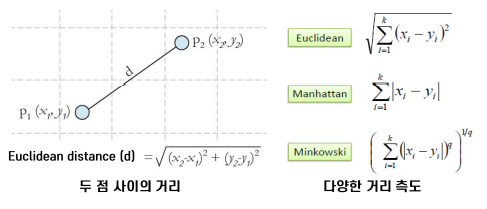
• 두 관측치 사이 의 거리를 측정하는 방법
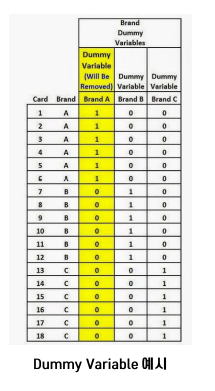
• 범주형 변수는 Dummy variable로 변환하여 거리 계산.

• KNN은 Lazy Algorithm으로 불림.
• 실시간적으로 빅데이터를 KNN으로 적용하기 어려운점이 있음.

K의 영향

• KNN의 Hyperparameter : K의 수, 거리 측정 방법
  • K는 모형의 복잡도를 결정, 거리는 어떤 가정을 가지고서 측정을 해줄것인가를 결정.
  • Validation Dataset을 이용해서 테스트를 하면서 결정
• K가 클수록 Underfitting, 작을 수록 Overfitting이 일어날 수 있다.

Logistic Regression

Logistic Regression의 배경

• 다중 선형회귀 분석
  • 목적 : 수치형 설명변수 X와 종속변수 Y간의 관계를 선형으로 가정하고 이를 가장 잘 표현할 수 있는 회귀계수를 추정
• 선형회귀모형의 Calssification버전이라 생각하면 됨.

예제

• 33명의 성인 여성에 대한 나이와 혈압 사이의 관계

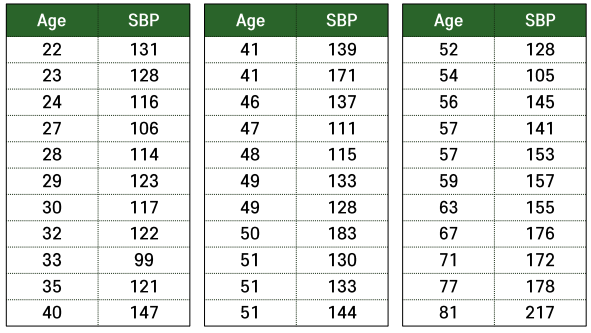
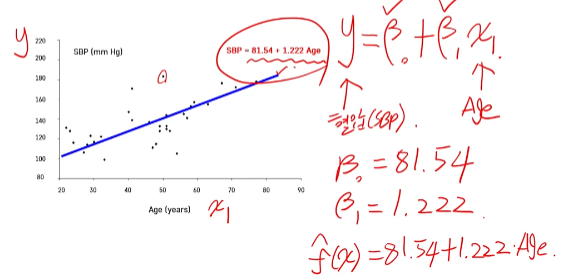
Logistic Regression의 필요성

• Logistic function을 활용하는 Linear Regression 모형
• 범주형 반응 변수
  • 이진변수
  • 멀티변수
• 일반 회귀분석과는 다른 방식으로 접근해야 함.

종속변수의 속성이 이진변수일때(0 or 1, ex : 불량품 0 양품 1, 높으면 1 낮으면 0, 강아지 1 고양이 0)

• 질문 : 확률값을 선형회귀분석의 종속변수로 사용하는 것이 타당한가?
• 답변 : 선형회귀분석의 우변은 범위에 대한 제한이 없기 때문에 우변과 좌변의 범위가 다른 문제점이 발생함.