Complex Matrix 실습, 딥러닝 기초

⚠️ 해당 내용은 멋쟁이사자처럼 AI School 오늘코드 박조은 강사의 자료를 토대로 정리한 내용입니다.

지난 포스트 에서 이어짐

Complex Matrix

F1 Score

• 정밀도와 재현율은 둘 중 하나만 채용해서는 예측 성능 평가 지표로 불완전(trade off 관계)
• F1 점수는 정밀도와 재현율의 조화평균
  • 정밀도와 재현율 둘다 높이면 F1 점수가 올라감

Precision-Recall Tradeoff

• 정밀도와 재현율은 상호보완적(Tradeoff)인 지표
• 예측한 것 중에서 거짓이었던 경우를 줄이려면, 더 확실한 경우에만 참으로 예측
• threshold(임계점)를 올리면 더 확실한 경우에만 참으로 판단
  • precision을 올릴 수 있지만 참으로 판단하는 경우가 줄어들게 되므로 recall은 내려감
  • 반대로 threshold를 내리면 recall은 올라가고 precision은 내려감

ROC curve

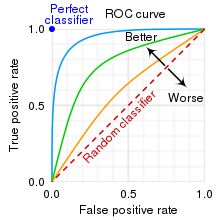
• $TPR = TP/(TP + FN), FPR = FP/(FP+TN)$
• Threshold에 따라서 달라지는 TP rate와 FP rate를 표시한 그래프
• ROC 커브가 TP rate 1, FP rate 0에 가까워질수록 더 좋은 모델
• 현실적으로 FP rate를 최대한 적게, TP rate를 높이는 것이 목표

AUC

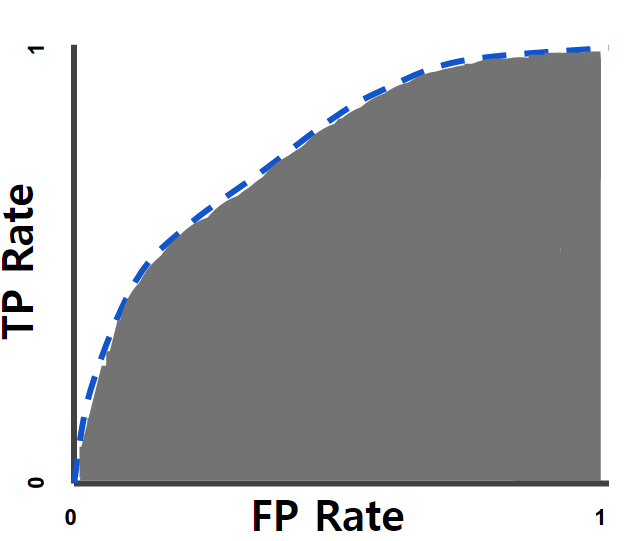
• AUC(area under curve)는 ROC 커브 아래의 곡면의 넓이를 의미

• AUC가 넓을수록 더 좋은 머신러닝 모델

  AUC=1	제대로 예측
  AUC=0.7	임계값에 따라 정밀도와 재현율이 달라짐여기에서는 0.5보다 크면 양성, 0.5보다 작으면 음성으로 예측
  AUC=0.5	두 선이 겹쳐서 제대로 된 예측력을 갖지 못함
  AUC=0	완전히 반대로 예측

SMOTE

Resampling

• 현실 세계의 데이터는 불균형한 데이터가 매우 많다
• 이러한 경우 어떻게 대처해야 하는가?

Under-sampling 과 Over-sampling

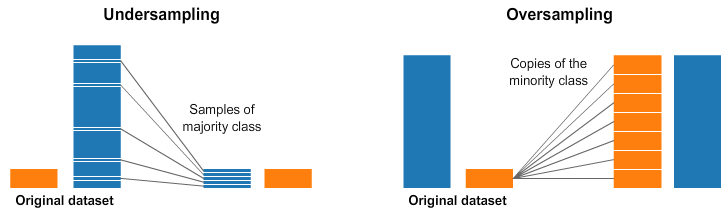
• 출처 : [Resampling strategies for imbalanced datasets

  Kaggle](https://www.kaggle.com/code/rafjaa/resampling-strategies-for-imbalanced-datasets/notebook)

• under-sampling은 더 값이 많은 쪽에서 일부만 샘플링하여 비율을 맞춰주는 방법.
  • under-sampling은 구현이 쉽지만 전체 데이터가 줄어 머신러닝 모델 성능이 떨어질 우려가 있다.
• over-sampling은 더 값이 적은 쪽에서 값을 늘려 비율을 맞춰준 방법.
  • over-sampling은 어떻게 없던 값을 만들어야 하는지에 대한 어려움이 존재한다.

Over-Sampling

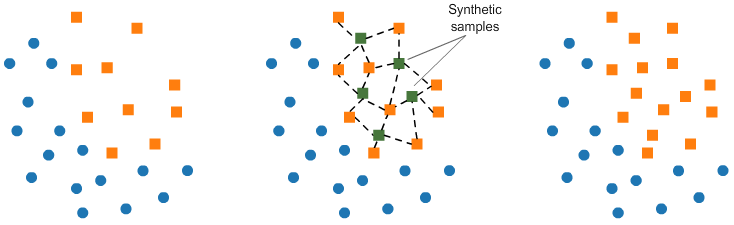
• SMOTE는 Synthetic Minority Over-sampling Technique의 약자
• 적은 값을 늘릴 때, k-근접 이웃의 값을 이용하여 합성된 새로운 값을 추가한다.
• k-근접 이웃이란 가장 가까운 k개 이웃을 의미한다.
• 새로 생성된 값은 좌표평면으로 나타냈을 때, k-근접 이웃의 중간에 위치하게 된다.

Credit Card Fraud Detection 실습

데이터 로드

import pandas as pd
import seaborn as sns

# pandas가 모든 열을 표시하도록 옵션을 변경한다.
pd.set_option('display.max_columns', None)

# creditcard.csv를 df로 할당한다
df = pd.read_csv("creditcard.csv")
df

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	V10	V11	V12	V13	V14	V15	V16	V17	V18	V19	V20	V21	V22	V23	V24	V25	V26	V27	V28	Amount	Class
0	0.0	-1.359807	-0.072781	2.536347	1.378155	-0.338321	0.462388	0.239599	0.098698	0.363787	0.090794	-0.551600	-0.617801	-0.991390	-0.311169	1.468177	-0.470401	0.207971	0.025791	0.403993	0.251412	-0.018307	0.277838	-0.110474	0.066928	0.128539	-0.189115	0.133558	-0.021053	149.62	0
1	0.0	1.191857	0.266151	0.166480	0.448154	0.060018	-0.082361	-0.078803	0.085102	-0.255425	-0.166974	1.612727	1.065235	0.489095	-0.143772	0.635558	0.463917	-0.114805	-0.183361	-0.145783	-0.069083	-0.225775	-0.638672	0.101288	-0.339846	0.167170	0.125895	-0.008983	0.014724	2.69	0
2	1.0	-1.358354	-1.340163	1.773209	0.379780	-0.503198	1.800499	0.791461	0.247676	-1.514654	0.207643	0.624501	0.066084	0.717293	-0.165946	2.345865	-2.890083	1.109969	-0.121359	-2.261857	0.524980	0.247998	0.771679	0.909412	-0.689281	-0.327642	-0.139097	-0.055353	-0.059752	378.66	0
3	1.0	-0.966272	-0.185226	1.792993	-0.863291	-0.010309	1.247203	0.237609	0.377436	-1.387024	-0.054952	-0.226487	0.178228	0.507757	-0.287924	-0.631418	-1.059647	-0.684093	1.965775	-1.232622	-0.208038	-0.108300	0.005274	-0.190321	-1.175575	0.647376	-0.221929	0.062723	0.061458	123.50	0
4	2.0	-1.158233	0.877737	1.548718	0.403034	-0.407193	0.095921	0.592941	-0.270533	0.817739	0.753074	-0.822843	0.538196	1.345852	-1.119670	0.175121	-0.451449	-0.237033	-0.038195	0.803487	0.408542	-0.009431	0.798278	-0.137458	0.141267	-0.206010	0.502292	0.219422	0.215153	69.99	0
…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…
284802	172786.0	-11.881118	10.071785	-9.834783	-2.066656	-5.364473	-2.606837	-4.918215	7.305334	1.914428	4.356170	-1.593105	2.711941	-0.689256	4.626942	-0.924459	1.107641	1.991691	0.510632	-0.682920	1.475829	0.213454	0.111864	1.014480	-0.509348	1.436807	0.250034	0.943651	0.823731	0.77	0
284803	172787.0	-0.732789	-0.055080	2.035030	-0.738589	0.868229	1.058415	0.024330	0.294869	0.584800	-0.975926	-0.150189	0.915802	1.214756	-0.675143	1.164931	-0.711757	-0.025693	-1.221179	-1.545556	0.059616	0.214205	0.924384	0.012463	-1.016226	-0.606624	-0.395255	0.068472	-0.053527	24.79	0
284804	172788.0	1.919565	-0.301254	-3.249640	-0.557828	2.630515	3.031260	-0.296827	0.708417	0.432454	-0.484782	0.411614	0.063119	-0.183699	-0.510602	1.329284	0.140716	0.313502	0.395652	-0.577252	0.001396	0.232045	0.578229	-0.037501	0.640134	0.265745	-0.087371	0.004455	-0.026561	67.88	0
284805	172788.0	-0.240440	0.530483	0.702510	0.689799	-0.377961	0.623708	-0.686180	0.679145	0.392087	-0.399126	-1.933849	-0.962886	-1.042082	0.449624	1.962563	-0.608577	0.509928	1.113981	2.897849	0.127434	0.265245	0.800049	-0.163298	0.123205	-0.569159	0.546668	0.108821	0.104533	10.00	0
284806	172792.0	-0.533413	-0.189733	0.703337	-0.506271	-0.012546	-0.649617	1.577006	-0.414650	0.486180	-0.915427	-1.040458	-0.031513	-0.188093	-0.084316	0.041333	-0.302620	-0.660377	0.167430	-0.256117	0.382948	0.261057	0.643078	0.376777	0.008797	-0.473649	-0.818267	-0.002415	0.013649	217.00	0

284807 rows × 31 columns

데이터 확인

# info
df.info()

• 결과값:

<class ‘pandas.core.frame.DataFrame’> RangeIndex: 284807 entries, 0 to 284806 Data columns (total 31 columns): # Column Non-Null Count Dtype
— —— ————– —–
0 Time 284807 non-null float64 1 V1 284807 non-null float64 2 V2 284807 non-null float64 3 V3 284807 non-null float64 4 V4 284807 non-null float64 5 V5 284807 non-null float64 6 V6 284807 non-null float64 7 V7 284807 non-null float64 8 V8 284807 non-null float64 9 V9 284807 non-null float64 10 V10 284807 non-null float64 11 V11 284807 non-null float64 12 V12 284807 non-null float64 13 V13 284807 non-null float64 14 V14 284807 non-null float64 15 V15 284807 non-null float64 16 V16 284807 non-null float64 17 V17 284807 non-null float64 18 V18 284807 non-null float64 19 V19 284807 non-null float64 20 V20 284807 non-null float64 21 V21 284807 non-null float64 22 V22 284807 non-null float64 23 V23 284807 non-null float64 24 V24 284807 non-null float64 25 V25 284807 non-null float64 26 V26 284807 non-null float64 27 V27 284807 non-null float64 28 V28 284807 non-null float64 29 Amount 284807 non-null float64 30 Class 284807 non-null int64
dtypes: float64(30), int64(1) memory usage: 67.4 MB

# 결측치를 확인.
df.isnull().sum()

• 결과값 : Time 0 V1 0 V2 0 V3 0 V4 0 V5 0 V6 0 V7 0 V8 0 V9 0 V10 0 V11 0 V12 0 V13 0 V14 0 V15 0 V16 0 V17 0 V18 0 V19 0 V20 0 V21 0 V22 0 V23 0 V24 0 V25 0 V26 0 V27 0 V28 0 Amount 0 Class 0 dtype: int64

Target 분포

우리가 찾는 class의 분포도를 확인해보도록 한다.

# Class (value_counts)
df["Class"].value_counts()

• 결과값 : 0 284315 1 492 Name: Class, dtype: int64

0과 1의 클래스로 구분되어있는데 데이터가 상당히 편중되어 있는 모습을 확인할 수 있다. Normalize 처리를 해주고, value_counts를 시각화해보자.

# "Class" value_counts normalize=True
df["Class"].value_counts(normalize = True)

• 결과값: 0 0.998273 1 0.001727 Name: Class, dtype: float64

# countplot 시각화
sns.countplot(data = df, x = "Class")

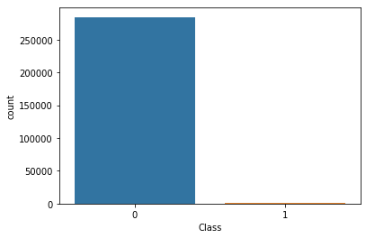
독립변수(문제)와 종속변수(정답) 분리

학습을 용이하게 하기 위해서 독립변수와 종속변수를 지정해주고 train과 test set을 만들어주도록 한다.

# input으로 들어갈 X와 기대값인 y를 분리한다.
# X에는 예측할 값인 "Class"를 제외한 값이 들어가야 한다.
# y에는 예측할 값인 "Class"만 들어가야 한다.

label_name = "Class"
X = df.drop(columns = label_name)
y = df[label_name]

X.shape, y.shape

• 결과값 : ((284807, 30), (284807,))

train_test_split

# X와 y값을 학습용 데이터와 검증용 데이터로 나눈다.(train_test_split)
# X_train, X_test, y_train, y_test에 값을 반환받는다.
# stratify : 원래 데이터의 값 비율대로 학습용 데이터와 검증용 데이터를 분할시켜준다.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y, random_state = 42)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

• 결과값: ((227845, 30), (56962, 30), (227845,), (56962,))

나눠진 셋의 비율을 확인해보도록 한다.

print(y_train.value_counts(1))
print(y_test.value_counts(1))

• 결과값: 0 0.998271 1 0.001729 Name: Class, dtype: float64 0 0.99828 1 0.00172 Name: Class, dtype: float64

Confusion matrix

DecisionTreeClassifier

결정트리 모델을 불러오고 학습 및 예측까지 진행하도록 한다.

# 모델 불러오기
from sklearn.tree import DecisionTreeClassifier

model= DecisionTreeClassifier(random_state = 42)

# 학습
model.fit(X_train, y_train)

# 예측
y_pred = model.predict(X_test)
y_pred[:5]

• 결과값 : array([0, 0, 0, 0, 0])

# predict_proba는 확률값을 예측한다.
# 각 클래스 마다의 확률을 예측한다.
# 0, 1 일 때 각각의 확률을 의미한다.
# [0.5, 0.5], [0.3, 0.7], [0.7, 0.3]등 형식으로 나온다.
# 클래스가 여러 종류일 때 확률을 사용해서 예측을 하기도 한다.

y_pred_proba = model.predict_proba(X_test)
y_pred_proba[:5]

• 결과값: array([[1., 0.], [1., 0.], [1., 0.], [1., 0.], [1., 0.]])

# np.argmax : 값이 가장 큰 인덱스를 반환한다.
import numpy as np
y_pred_proba_class = np.argmax(y_pred_proba, axis = 1)
y_pred_proba_class

• 결과값 : array([0, 0, 0, …, 0, 0, 0])

# predict 로 예측한 결과값과 predict_proba 로 예측한 결과값을 비교해본다.
(y_pred == y_pred_proba_class).mean()

• 결과값: 1.0

# 예측 결과의 unique 값
np.unique(y_pred)

• 결과값 : array([0, 1])

# 정확도
(y_test == y_pred).mean()

• 결과값 : 0.9991397773954567

# crosstab
pd.crosstab(y_test, y_pred)

col_0	0	1
Class
0	56840	24
1	25	73

confusion matrix를 사용해보도록 하자.

# confusion_matrix
from sklearn.metrics import confusion_matrix

cf = confusion_matrix(y_test, y_pred)
cf

• 결과값 : array([[56840, 24], [ 25, 73]])

# heatmap으로 시각과
sns.heatmap(cf, annot = True, cmap = "Blues")

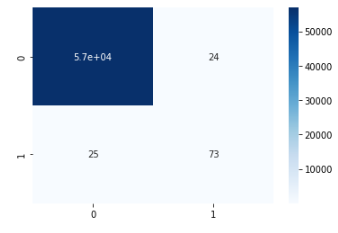
ConfusionMatrixDisplay 기능을 사용해서도 시각화를 시도해보도록 한다.

from sklearn.metrics import ConfusionMatrixDisplay

ConfusionMatrixDisplay(cf).plot()

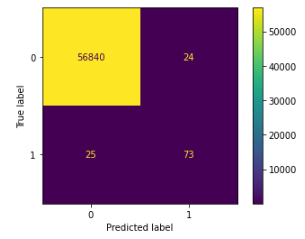
classification_report를 사용해서 precision, recall, f1-score을 계산해보도록 한다.

# classification_report
from sklearn.metrics import classification_report

print(classification_report(y_test, y_pred, target_names = ['0', '1']))

결과값:

							precision    recall  f1-score   support

           0       1.00      1.00      1.00     56864
           1       0.75      0.74      0.75        98

    accuracy                           1.00     56962
   macro avg       0.88      0.87      0.87     56962
weighted avg       1.00      1.00      1.00     56962

이번에는 accuracy, precision, recall, f1-score를 직접 구해보도록 하자

# accuracy
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))

# f1_score
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred))

# precision_score
from sklearn.metrics import precision_score
print(precision_score(y_test, y_pred))

# recall_score
from sklearn.metrics import recall_score
print(recall_score(y_test, y_pred))

• 결과값: 0.9991397773954567 0.7487179487179487 0.7525773195876289 0.7448979591836735

데이터 샘플링

Under-Sampling

1인 데이터가 492개이기 대문에 0인 데이터를 랜덤하게 492개 추출하면 언더샘플링이다.

y.value_counts()

• 결과값: 0 284315 1 492 Name: Class, dtype: int64

df_0 = df[df["Class"] == 0].sample(492)
df_1 = df[df["Class"]==1]

df_0.shape, df_1.shape

• 결과값 : ((492, 31), (492, 31))

df_under = pd.concat([df_0, df_1])
df_under["Class"].value_counts()

• 결과값: 0 492 1 492 Name: Class, dtype: int64

Over-Sampling

SMOTE를 불러와서 over-sampling을 시도해보도록 한다.

# SMOTE는 Synthetic Minority Over-sampling Technique의 약자로 합성 소수자 오버샘플링 기법
# X, y를 학습하고 다시 샘플링한다(fit_resample).
from imblearn.over_sampling import SMOTE

sm = SMOTE(random_state = 42)
X_resample, y_resample = sm.fit_resample(X,y)

# X shape

X.shape, X_resample.shape

• 결과값 : ((284807, 30), (568630, 30))

# Y shape

y.shape, y_resample.shape

• 결과값 : ((284807,), (568630,))

# y의 value_counts
y.value_counts()

• 결과값: 0 284315 1 492 Name: Class, dtype: int64

# y_resample의 value_counts
y_resample.value_counts()

• 결과값: 0 284315 1 284315 Name: Class, dtype: int64

value_counts()를 비교한 결과, 리샘플링한 y에서 클래스의 불균형이 해소가 된 것을 확인할 수 있다. 리샘플링된 데이터들을 이용해서 다시 학습 셋을 나눠주고 학습 및 예측을 진행하고 metric점수까지 확인하도록 하자.

# 데이터 분리
# 변수명이 바뀌기 때문에 stratify=y_resample로 변경해줘야 정상적으로 작동한다.

X_train, X_test, y_train, y_test = train_test_split(X_resample, y_resample, test_size=0.2, stratify=y_resample, random_state = 42)

display(y_train.value_counts())
display(y_test.value_counts())

• 결과값: 0 227452 1 227452 Name: Class, dtype: int64 1 56863 0 56863 Name: Class, dtype: int64

학습과 예측을 진행하는 과정은 리샘플링 하기 전 데이터와 동일한 방법으로 진행하기 때문에 코드는 생략하도록 하겠다. 리샘플링 한 후, metric 지표들을 확인해보자.

# 정확도
(y_pred == y_test).mean()

• 결과값 : 0.99847000685859

# classification_report
print(classification_report(y_test, y_pred))

• 결과값: precision recall f1-score support

       0       1.00      1.00      1.00     56863
       1       1.00      1.00      1.00     56863
  

  accuracy 1.00 113726 macro avg 1.00 1.00 1.00 113726 weighted avg 1.00 1.00 1.00 113726

# accuracy
print(accuracy_score(y_test, y_pred))

# f1_score
print(f1_score(y_test, y_pred))

# precision_score
print(precision_score(y_test, y_pred))

# recall_score
print(recall_score(y_test, y_pred))

• 결과값: 0.99847000685859 0.9984707598741454 0.9979795850243328 0.9989624184443311

리샘플링 전(0.7487179487179487)과 후(0.9984707598741454)의 F1 Score(불균형한 데이터셋을 평가할 때 참고하는 지포)를 비교할 때 점수가 확연히 오른 것을 확인할 수 있다.

딥러닝 기초

머신러닝과 딥러닝

• 인간 개입의 여부
  • 머신러닝 : 인간이 직접 특징을 도출할 수 있도록 설계하여 예측값 출력
  • 딥러닝 : 인공지능 스스로 일정 범주의 데이터를 바탕으로 공통된 특징을 도출하고 특징을 예측값으로 출력 ⇒ 사람같지만 보다 빠른 학습속도, 원하는 빅데이터를 학습 후 활용 가능

초기 인공신경망 : 퍼셉트론(Perceptron)

• 사람의 뉴런을 본따서 만든 개념
• 퍼셉트론은 두 개의 노드가 있을 경우, 그 두 개의 노드가 각각 들어가야 하는 위치인 입력치와 그를 가중하는 가중치, 이를 통해 계산하여 나온 결과인 출력 값으로 구성

단층 퍼셉트론

• 입력층과 출력층으로 구성
• 하나의 선으로 0과 1을 분리하지 못함 → 단층 퍼셉트론의 합계

순전파와 역전파

Model architecture

• 출처 : Deep learning on MNIST — NumPy Tutorials

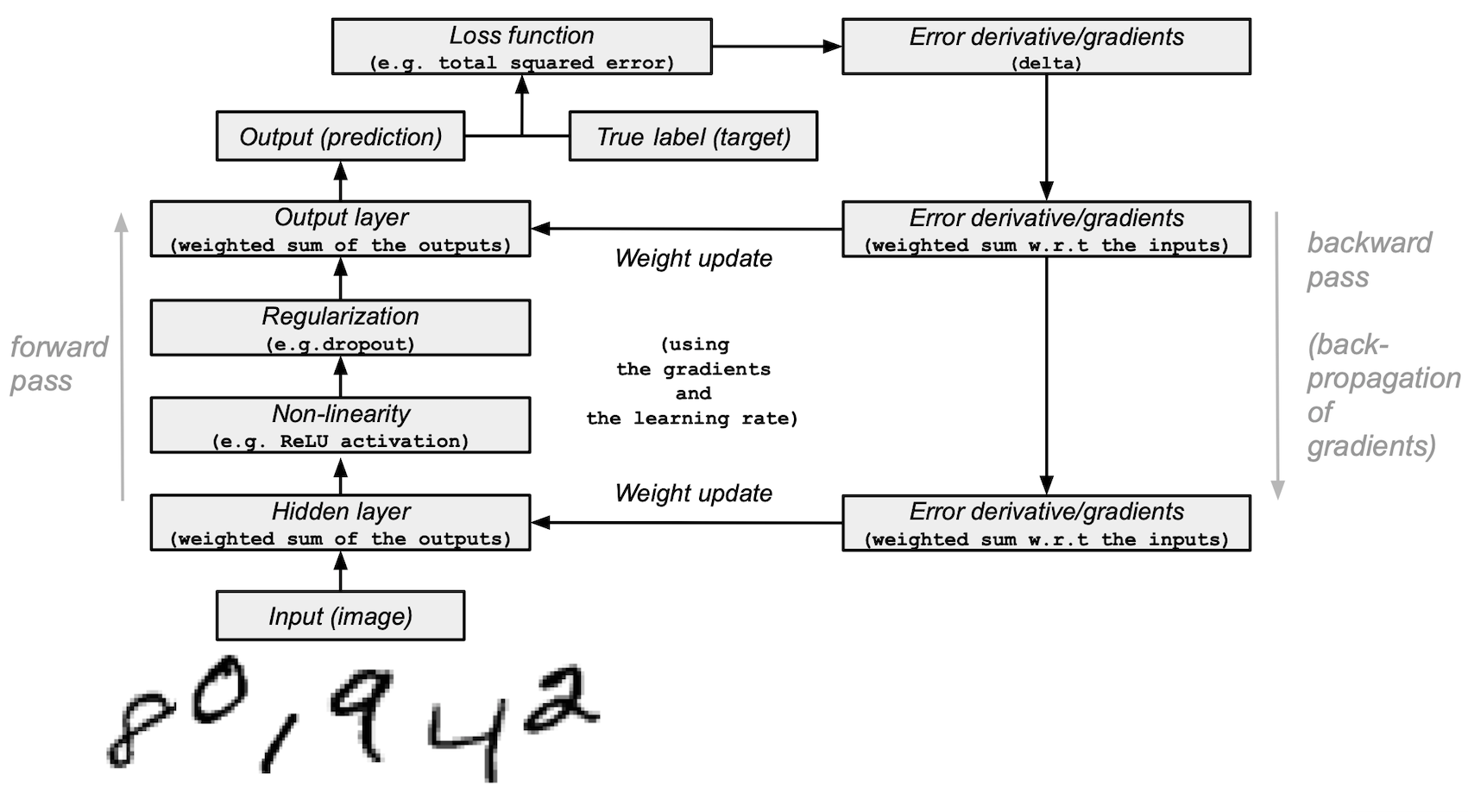
딥러닝의 연산 : 순전파(Forward Propagation)

• 인공신경망에서 입력층에서 출력층 방향으로 예측값의 연산이 진행되는 과정
• 입력값은 입력층, 은닉층을 지나며 각 층에서 가중치와 함께 연산되어 출력층에서 연산을 마친 예측값을 도출

역전파(Backpropagtion)

• 역전파, 오차 역전파법 또는 오류 역전파 알고리즘은 다층 퍼셉트론 학습에 사용되는 통계적 기법
• 출력층에서 제시한 값이 실제 원하는 값에 가까워지도록 학습하기 위한 통계적 방법에 의한 오차 역전법을 사용
• 입력층에 대해 원하는 값이 출력되도록 각각의 가중치를 조정하는 방법으로 사용. 속도는 느리지만 안정적인 결과를 얻을 수 있어 기계학습에 널리 사용

활성화 함수

• 은닉층과 출력층의 뉴런에서 출력값을 결정하는 함수로 가중치를 생성

활성화 함수 : Sigmoid

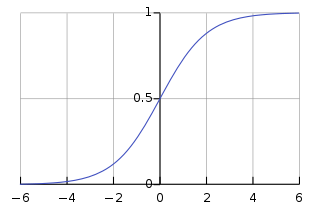
• 출처 : 시그모이드 함수 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
• S자형 곡선을 갖는 수학 함수(ex 로지스틱 함수)
• 장점 : 모델 제작 소요 시간을 줄임
• 단점 : 미분 범위가 짧아 정보가 손실(Gradient Vanishing 현상)됨
• 활용 : 로지스틱 함수, 이진 분류 등

활성화 함수 : tanh - 하이퍼볼릭탄젠트함수*

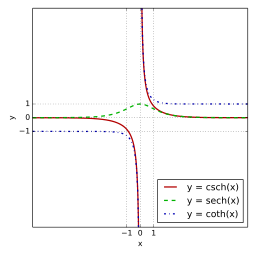
• 출처 : 쌍곡선 함수 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
• 쌍곡선 함수 중 하나. 시그모이드를 대체할 수 있는 활성화 함수
• 데이터 중심을 0으로 위치시키는 효과가 있기 때문에 다음 층의 학습이 더 쉽게 이루어짐
• 미분 범위가 짧사 정보가 손실됨

Sigmoid, tanh

• S 자 형태의 비슷한 특징
• 일정 범위를 벗어낫을 때 기울기가 0이 되어 기울기 소실(Gradient Vanishing) 문제가 발생

Gradient Vanishing

• Gradient Vanishing : 깊은 인공신경망 학습을 할 때 역전파 과정에서 입력층으로 갈수록 기울기가 점차 작아지는 현상. 입력층에 가까운 층들에서 가중치들이 업데이트가 제대로 되지 않으면 결국 최적의 모들을 찾을 수 없음. ANN 신경망의 문제점으로 대두
• Gradient Exploding : 가중치들이 비정상적으로 큰 값이 되면서 발산. RNN에서 쉽게 발생

활성화 함수 : ReLU

• 기울기 소실을 완화하는 가장 간단한 방법으로 은닉층의 활성화 함수를 ReLU나 leaky ReLU를 사용.
• 하지만 단점으로는, Dying ReLU현상(x가 0보다 작으면 항상 동일한 0값을 출력)이 있음

활성화 함수 : leaky ReLU

• ReLU함수의 단점인 Dying ReLU 현상을 개선

딥러닝의 학습과정

딥러닝의 학습과정

• 출력값과 실제값을 비교하여 그 차이를 최소화하는 가중치w(weight)와 편향b(bias)의 조합 찾기
• 가중치는 오차를 최소화하는 방향으로 모델이 스스로 탐색(역전파)
• 오차계산은 실제 데이터를 비교하며 손실함수를 최소화하는 값을 탐색 ⇒ 알맞은 손실함수의 선정이 중요
  • 손실함수 : 모델의 예측값과 사용자가 원하는 실제값의 오차
• 손실함수를 찾아 최소화하기 위한 방법으로는 경사하강법이 존재하며, 옵티마이저로 경사하강법을 원리를 이용
  • 옵티마이저 : 최적화 방식을 결정해주는 방식. 경사하강법에 기반을 둠