딥러닝: 회귀
⚠️ 해당 내용은 멋쟁이사자처럼 AI School 오늘코드 박조은 강사의 자료를 토대로 정리한 내용입니다.
Pima TF classification
예측
y_pred = model.predict(X_test)
y_pred
위 코드대로 하면 세로로 코드가 매우 길게 나온다. 좀더 보기 좋은 시각화를 하기 위해 flatten()을 사용하도록 한다.
# 예측값 시각화
# 임계값을 정해서 특정값 이상이면 True, 아니면 False로 변환해서 사용할 예정.
# Precision-Recall Tradeoff의 threshold를 적용시켜준다고 생각하면 된다.
y_predict = (y_pred.flatten() > 0.5).astype(int)
y_predict

flatten한 데이터를 토대로 정확도를 직접 계산해보자
(y_test == y_predict).mean()
💡 작성한 모델들을 tweek해서 모델을 다양하게 구성해서 점수 향상을 노려보도록 하자.
- dropout은 layer마다 얼마나 떨어뜨릴 것인지를 정한다. 사용한 layer가 여러 개면 dropout을 해당 layer 바로 밑에 추가적으로 작성해도 된다.
- loss => W(가중치), b(편향) 값을 업데이트 해주기 위해 사용하고, metric 모델의 성능을 평가
- 분류에서 사용하는 loss :
- 이진분류 - binarycrossentropy 다중분류 : 원핫인코딩 - categorical_crossentropy 다중분류 : 오디널 - sparse_categorical_crossentropy
- 분류에서 사용하는 loss :
🤔 머신러닝과 딥러닝을 했을 때 어느쪽이 성능이 더 좋았는가?
비슷하며 큰 차이를 느끼지 못했다. 그 이유는 보통은 정형데이터는 딥러닝보다는 머신러닝이 대체적으로 좋은 성능을 낼때가 있기 때문이다. 무엇보다도 중요한 것은 데이터 전처리와 피처엔지니어링이 성능에 더 많은 영향을 주게 된다.
⚠️garbage in garbage out => 좋은 데이터를 통해 모델을 만드는게 성능에 가장 중요한 역할을 한다!
기본 회귀: 연비 예측
아래 실습은 구글의 Tensorflow 튜토리얼 문서 중 회귀 파트이다. 자세한 정보를 확인하려면 상단 제목을 클릭하면 이동한다. 정규화 전 과정은 해당 문서를 참고하도록 하자.
정규화
train_dataset.describe().transpose()[['mean', 'std']]
| mean | std | |
|---|---|---|
| MPG | 23.310510 | 7.728652 |
| Cylinders | 5.477707 | 1.699788 |
| Displacement | 195.318471 | 104.331589 |
| Horsepower | 104.869427 | 38.096214 |
| Weight | 2990.251592 | 843.898596 |
| Acceleration | 15.559236 | 2.789230 |
| Model Year | 75.898089 | 3.675642 |
| Europe | 0.178344 | 0.383413 |
| Japan | 0.197452 | 0.398712 |
| USA | 0.624204 | 0.485101 |
정규화 레이어
keras에서는 정규화를 해주는 명령어가 있다.
normalizer = tf.keras.layers.Normalization(axis=-1)
그런 다음 Normalization.adapt를 호출하여 전처리 레이어의 상태를 데이터에 맞춘다.
normalizer.adapt(np.array(train_features))
# 평균과 분산을 계산하고 레이어에 저장
print(normalizer.mean.numpy())
결과값:
[[ 5.478 195.318 104.869 2990.252 15.559 75.898 0.178 0.197
0.624]]
# 레이어가 호출되면 각 특성이 독립적으로 정규화된 입력 데이터를 반환
first = np.array(train_features[:1])
with np.printoptions(precision=2, suppress=True):
print('First example:', first)
print()
print('Normalized:', normalizer(first).numpy())
선형회귀
- 심층 신경망 모델을 구축하기 전에 하나 및 여러 변수를 사용하는 선형 회귀부터 시작한다.
하나의 변수를 사용한 선형 회귀
- 단일 변수 선형 회귀로 시작하여
'Horsepower'에서'MPG'를 예측 tf.keras를 사용하여 모델을 교육할 때는 일반적으로 모델 아키텍처를 정의하는 것으로 시작한다. 일련의 단계를 나타내는tf.keras.Sequential모델을 사용한다.tf.keras.layers.Normalization전처리 레이어를 사용하여'Horsepower'입력 특성을 정규화 한다.-
선형 변환()을 적용하여 선형 레이어(
tf.keras.layers.Dense)로 1개의 출력을 생성한다.y=mx+b
- 입력의 수는
input_shape인수로 설정하거나 모델이 처음 실행될 때 자동으로 설정할 수 있다.
먼저 'Horsepower'특성으로 구성된 NumPy 배열을 만든 후, tf.keras.layers.Normalization을 인스턴스화하고 상태를 horsepower데이터에 맞춘다.
# 사이킷런의 전처리 기능이나 직접 계산을 통해 정규화를 해주는 방법도 있다.
# TF에서도 정규화 하는 기능을 제공한다.
# horsepower_normalizer : Horsepower 변수를 가져와서 해당 변수만 정규화
horsepower = np.array(train_features['Horsepower'])
horsepower_normalizer = layers.Normalization(input_shape=[1,], axis=None)
horsepower_normalizer.adapt(horsepower)
Keras 순차 모델 빌드한다.
# 전처리 레이어를 추가해서 모델을 만들 때 전처리 기능을 같이 넣어 줄 수 있다.
# 장점 : 정규화 방법을 모르더라도 추상회된 기능을 사용해서 쉽게 정규화 할 수 있다.
# 단점 : 소스코드, 문서를 열어보기 전에는 추상화된 기능이 어떤 기능인지 알기 어렵다.
# 사이킷런의 pipeline 기능과 유사.
# 활성함수를 적지 않으면 'linear(y = x)'가 defalut로 적용된다.
horsepower_model = tf.keras.Sequential([
horsepower_normalizer,
layers.Dense(units=1)
])
horsepower_model.summary()
Untitled 
🤔 레이어 구성에서 출력층의 분류와 회귀의 차이?
- 분류는(n, activation=’softmax’), (1, activation=’sigmoid’) 이 있는데 회귀는 항등함수
- 항등함수 : 입력받은 값을 그대로 출력하는 함수
- 회귀의 출력층은 현재까지 계산된 값을 그대로 출력해야하기 때문에 항등함수를 사용하여 현재까지 계산된 값을 그대로 출력
- 회귀의 출력층은 항상
layers.Dense(units=1)형태로 나온다.
Keras Model.fit을 사용하여 100 epoch에 대한 훈련을 실행한다.
이 모델은 'Horsepower'로부터 'MPG'를 예측한다. 처음 10개의 ‘Horsepower’ 값에 대해 훈련되지 않은 모델을 실행한다. 결과는 좋지 않지만 예상되는 모양 (10, 1)을 가지고 있다.
horsepower_model.predict(horsepower[:10])
결과값:
1/1 [==============================] - 0s 104ms/step
array([[ 0.769],
[ 0.434],
[-1.419],
[ 1.078],
[ 0.975],
[ 0.383],
[ 1.155],
[ 0.975],
[ 0.254],
[ 0.434]], dtype=float32)
모델이 빌드되면 Model.compile메서드를 사용하여 훈련 절차를 구성한다. compile에 가장 중요한 인수는 loss및 optimizer이다. 이들이 최적화 대상(mean_absolute_error)과 방식(tf.keras.optimizers.Adam사용)을 정의하기 때문이다.
horsepower_model.compile(
# Adam(learning_rate = 0.1) : 분류와 다르게 learning rate를 설정해서 경사하강법의 하강을 조절
optimizer=tf.keras.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
%%time
history = horsepower_model.fit(
train_features['Horsepower'],
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
history객체에 저장된 통계를 사용하여 모델의 훈련 진행 상황을 시각화한다.
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
| loss | val_loss | epoch | |
|---|---|---|---|
| 95 | 3.803493 | 4.186892 | 95 |
| 96 | 3.804063 | 4.181873 | 96 |
| 97 | 3.804071 | 4.199119 | 97 |
| 98 | 3.805533 | 4.185143 | 98 |
| 99 | 3.803304 | 4.187895 | 99 |
def plot_loss(history):
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.ylim([0, 10])
plt.xlabel('Epoch')
plt.ylabel('Error [MPG]')
plt.legend()
plt.grid(True)
plot_loss(history)
Untitled 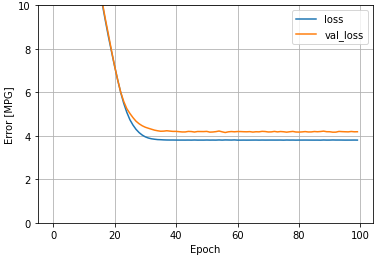
나중을 위해 테스트 세트에서 결과를 수집한다.
test_results = {}
test_results['horsepower_model'] = horsepower_model.evaluate(
test_features['Horsepower'],
test_labels, verbose=0)
단일 변수 회귀이므로 모델의 예측을 입력의 함수로 쉽게 볼 수 있다.
# linspace : x값을 임의로 생성
x = tf.linspace(0.0, 250, 251)
y = horsepower_model.predict(x)
def plot_horsepower(x, y):
plt.scatter(train_features['Horsepower'], train_labels, label='Data')
plt.plot(x, y, color='k', label='Predictions')
plt.xlabel('Horsepower')
plt.ylabel('MPG')
plt.legend()
plot_horsepower(x, y)
Untitled 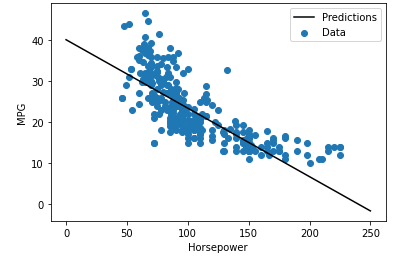
다중 입력이 있는 선형 회귀
이전에 정의하고 전체 데이터세트에 적용한 normalizer(tf.keras.layers.Normalization(axis=-1)
)의 첫 레이어를 사용하여 2단계 Keras Sequential 모델을 다시 생성한다.
linear_model = tf.keras.Sequential([
normalizer,
layers.Dense(units=1)
])
linear_model.predict(train_features[:10])
결과값 :
1/1 [==============================] - 0s 75ms/step
array([[-1.155],
[-0.724],
[ 0.703],
[ 0.384],
[ 1.115],
[-0.033],
[ 0.908],
[-2.392],
[-0.736],
[-0.436]], dtype=float32)
모델을 호출하면 가중치 행렬이 만들어집니다. kernel가중치(y=mx+b의 m)가 (9, 1)모양인지 확인한다.
linear_model.layers[1].kernel
결과값:
<tf.Variable 'dense_1/kernel:0' shape=(9, 1) dtype=float32, numpy=
array([[ 0.522],
[ 0.339],
[ 0.165],
[-0.153],
[-0.638],
[ 0.728],
[-0.507],
[ 0.506],
[-0.303]], dtype=float32)>
위 과정과 컴파일을 하고 동일하게 모델을 fit한다.
linear_model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.1),
loss='mean_absolute_error')
%%time
history = linear_model.fit(
train_features,
train_labels,
epochs=100,
# Suppress logging.
verbose=0,
# Calculate validation results on 20% of the training data.
validation_split = 0.2)
이 회귀 모델의 모든 입력을 사용하면 하나의 입력이 있는 horsepower_model보다 훨씬 더 낮은 훈련 및 검증 오류를 달성할 수 있다.
plot_loss(history)
Untitled 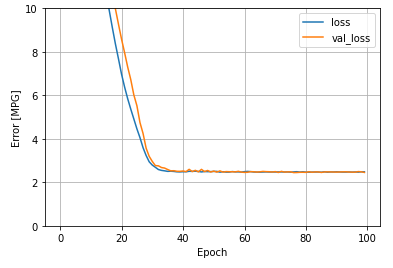
나중을 위해 테스트 세트에서 결과를 수집한다.
test_results['linear_model'] = linear_model.evaluate(
test_features, test_labels, verbose=0)
심층 신경망(DNN)을 사용한 회귀
이러한 모델에는 선형 모델보다 몇 개의 레이어가 더 포함된다.
- 이전과 같은 정규화 레이어(단일 입력 모델의 경우
horsepower_normalizer및 다중 입력 모델의 경우normalizer사용) - ReLU(
relu) 활성화 함수 비선형성이 있는 두 개의 숨겨진 비선형Dense레이어 - 선형
Dense단일 출력 레이어
두 모델 모두 동일한 훈련 절차를 사용하므로 compile 메서드는 아래의 build_and_compile_model 함수에 포함된다.
def build_and_compile_model(norm):
model = keras.Sequential([
norm,
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
model.compile(loss='mean_absolute_error',
optimizer=tf.keras.optimizers.Adam(0.001))
return model
DNN과 단일 입력을 사용한 회귀
입력으로 'Horsepower'만 사용하고 정규화 레이어로 horsepower_normalizer(앞서 정의)를 사용하여 DNN 모델 생성
dnn_horsepower_model = build_and_compile_model(horsepower_normalizer)
dnn_horsepower_model.summary()
Untitled 
fit으로 모델 훈련
%%time
history = dnn_horsepower_model.fit(
train_features['Horsepower'],
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
plot_loss(history)
선형 단일 입력 horsepower_model보다 약간 더 우수한 결과를 나타낸다.
Untitled 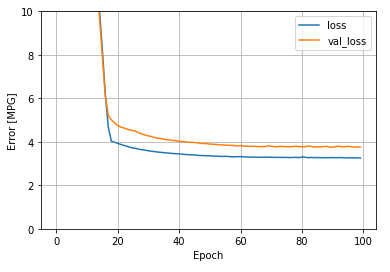
예측을 'Horsepower'의 함수로 플로팅하면 이 모델이 숨겨진 레이어에서 제공하는 비선형성을 어떻게 이용하는지 알 수 있다.
# linspace(0, 250, 251) : 0부터 251 사이에 251개의 값을 랜덤으로 생성
x = tf.linspace(0.0, 250, 251)
y = dnn_horsepower_model.predict(x)
plot_horsepower(x, y)
Untitled 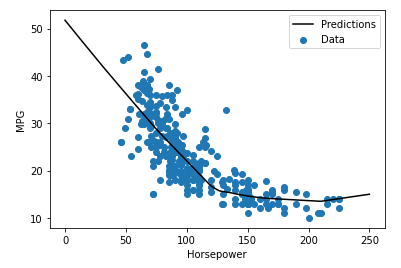
나중을 위해 테스트 세트에서 결과를 수집
test_results['dnn_horsepower_model'] = dnn_horsepower_model.evaluate(
test_features['Horsepower'], test_labels,
verbose=0)
DNN 및 다중 입력을 사용한 회귀
모든 입력을 사용하여 이전 결과들을 반복해준다.
dnn_model = build_and_compile_model(normalizer)
dnn_model.summary()
Untitled 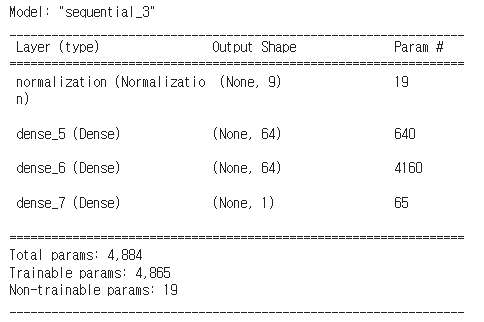
%%time
history = dnn_model.fit(
train_features,
train_labels,
validation_split=0.2,
verbose=0, epochs=100)
plot_loss(history)
Untitled 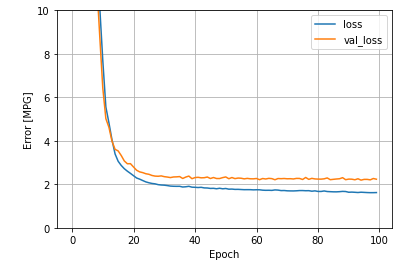
test_results['dnn_model'] = dnn_model.evaluate(test_features, test_labels, verbose=0)
성능
모든 모델의 테스트 성능을 검토해본다.
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
| Mean absolute error [MPG] | |
|---|---|
| horsepower_model | 3.646085 |
| linear_model | 2.497618 |
| dnn_horsepower_model | 2.928305 |
| dnn_model | 1.701235 |
예측하기
Keras Model.predict를 사용하여 테스트 세트에서 dnn_model로 예측을 수행하고 손실을 확인할 수 있다.
test_predictions = dnn_model.predict(test_features).flatten()
a = plt.axes(aspect='equal')
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
lims = [0, 50]
plt.xlim(lims)
plt.ylim(lims)
_ = plt.plot(lims, lims)
Untitled 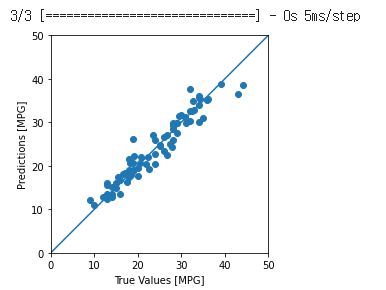
합리적으로 예측하는 것으로 보인다. 오류의 분포도 확인해보도로고 한다.
error = test_predictions - test_labels
plt.hist(error, bins=25)
plt.xlabel('Prediction Error [MPG]')
_ = plt.ylabel('Count')
Untitled 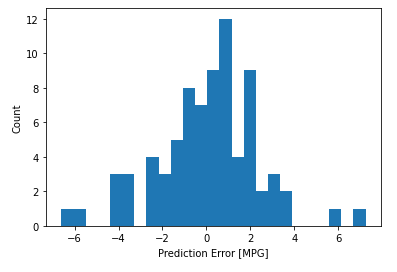
나중에 모델을 다시 사용할 수 있도록 모델을 저장해주자.
dnn_model.save('dnn_model')
#모델 다시 호출
reloaded = tf.keras.models.load_model('dnn_model')
test_results['reloaded'] = reloaded.evaluate(
test_features, test_labels, verbose=0)
pd.DataFrame(test_results, index=['Mean absolute error [MPG]']).T
| Mean absolute error [MPG] | |
|---|---|
| horsepower_model | 3.646085 |
| linear_model | 2.497618 |
| dnn_horsepower_model | 2.928305 |
| dnn_model | 1.701235 |
| reloaded | 1.701235 |
Regression 실습 데이터에서 보고자 하는 point
- 정형데이터 입력층 input_shape
- 정규화 레이어의 사용 => 직접 정규화해도 된다.
- 출력층이 분류와 다르게 구성이 된다는 점
- loss 설정이 분류, 회귀에 따라 다르다.
- 입력변수(피처)를 하나만 사용했을 때보다 여러 변수를 사용했을 때 성능이 더 좋아졌다. => 반드시 여러 변수를 사용한다라고 해서 성능이 좋아지지 않을 수도 있지만 너무 적은 변수로는 예측모델을 잘 만들기 어렵다는 점을 알수 있습니다.
🤔 loss와 val_loss의 차이는 뭔가요?
loss는 훈련 손실값, val_loss는 검증 손실값. model.fit에서 validation_split에서 지정해줄 수 있으며, 퍼센트로 지정해준다(ex. validation_split = 0.2 ⇒ validation set을 20%만큼 지정)
🤔 dnn_model.predict(test_features).flatten() 예측 결과 뒤에 flatten() 이 있는 이유는 무엇일까요?
2차원을 1차원으로 만들어 주기 위함이다. flatten()은 n차원을 1차원으로 만들어주는 역할을 한다.
🤔 신경망 모델 자체가 2차원 결과가 나오기로 만들어진건가요?
API 에서 제공하는 기능이라 사이킷런과 차이가 있습니다. 내부에서 사용하는 알고리즘의 원리는 비슷하지만 기능 구현에 차이가 있습니다. 논문을 작성할 때는 c, c++로 머신러닝, 딥러닝 알고리즘을 작성하기도 합니다. 텐서플로, 파이토치는 리서처도 사용하기는 하지만 프로덕트 개발 등을 위한 목적으로 만들어졌기 때문에 밑바닥부터 코드를 작성하는 것에 비해 간단한 API를 제공합니다. 또한, API 마다 기능의 차이가 있습니다. 사이킷런에서 정형데이터를 전처리하는 기능을 포함하고 있는 것처럼 텐서플로에서도 정형데이터, 이미지, 텍스트 등을 전처리하는 기능들도 포함하고 있습니다.
💡 Numpy 절대 기초 문서를 하루에 4~5박스 정도씩 TIL 정리하는 것을 추천
pima TF regression
라이브러리 import
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
데이터 확인
df = pd.read_csv("http://bit.ly/data-diabetes-csv")
df.shape
결과값 : (768, 9)
df.head()
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | Outcome |
|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 |
# Insulin 값이 0보다 큰 값만 사용한다.
df = df[df["Insulin"]>0].copy()
df.shape
결과값 : (394, 9)
학습 데이터 나누기
# label_name 을 Insulin 으로 설정.
label_name = "Insulin"
# train, test 데이터셋을 pandas 의 sample을 사용해서 8:2로 나눈다.
train = df.sample(frac=0.8, random_state = 42)
test = df.drop(train.index)
train.shape, test.shape
결과값 : ((315, 9), (79, 9))
# X, y set 만들기
X_train = train.drop(label_name, axis = 1)
y_train = train[label_name]
X_test = test.drop(label_name, axis = 1)
y_test = test[label_name]
X_train.shape, y_train.shape, X_test.shape, y_test.shape
결과값:
((315, 8), (315,), (79, 8), (79,))
딥러닝 레이어 만들기
# tensorflow 를 tf로 불러오기
import tensorflow as tf
# input_shape 값을 구한다. feature의 수로 만든다.
input_shape = X_train.shape[1]
input_shape
결과값 : 8
# 모델 빌드
model = tf.keras.models.Sequential([
# 입력 레이어를 Input 레이어로 사용할 수도 있다.
tf.keras.layers.Dense(128, input_shape=[input_shape]),
tf.keras.layers.Dense(128, activation='selu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(128, activation='selu'),
tf.keras.layers.Dropout(0.2),
# 모델 구성은 전체적으로 분류와 비슷하지만 회귀는 출력을 하나로 한다.
tf.keras.layers.Dense(1)
])
모델 컴파일
# 모델을 컴파일
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(optimizer=optimizer,
loss=['mae', 'mse'], metrics = ["mae", "mse"])
# 모델을 요약.
model.summary()
Untitled 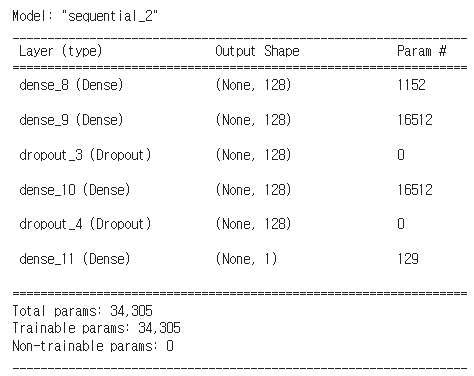
초기 model.summary()를 사용할 경우 위 이미지와 다르게 나올 수 있다. 해당 이미지는 여러 번의 수정을 거친 상황이기 때문이다.
학습
# 모델을 학습
# 학습결과를 history 변수에 할당
early_stop = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=100)
history = model.fit(X_train, y_train, validation_split=0.2, epochs=1000, verbose = 0, callbacks = [early_stop])
# history 를 데이터프레임으로 만듭니다.
df_hist = pd.DataFrame(history.history)
df_hist.tail(3)
| loss | mae | mse | val_loss | val_mae | val_mse | |
|---|---|---|---|---|---|---|
| 387 | 49.656857 | 49.656857 | 6215.549316 | 63.018036 | 63.018036 | 10140.137695 |
| 388 | 52.097633 | 52.097633 | 6365.834473 | 64.636993 | 64.636993 | 10197.075195 |
| 389 | 53.871567 | 53.871567 | 6537.537598 | 64.516808 | 64.516808 | 10913.817383 |
학습결과 시각화
# 학습결과를 시각화
df_hist[["loss", "val_loss"]].plot()
Untitled 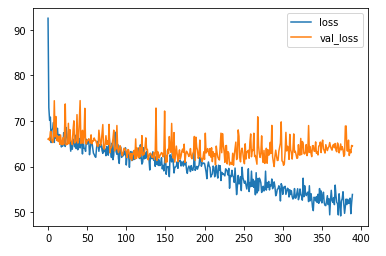
df_hist[['mae','val_mae']].plot()
Untitled 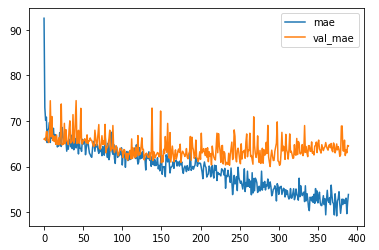
df_hist[['mse', "val_mse"]].plot()
Untitled 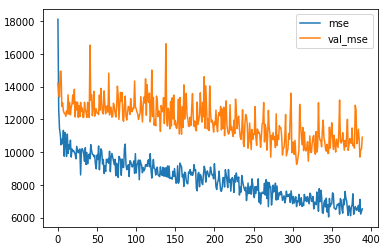
예측
학습한 모델에 X_test 데이터를 넣어 예측을 진행한다.
# y_pred
y_pred = model.predict(X_test)
y_pred[:5]
결과값:
3/3 [==============================] - 0s 6ms/step
array([[104.01402 ],
[139.20187 ],
[ 81.99638 ],
[ 60.604176],
[ 56.916958]], dtype=float32)
# 예측값을 flatten을 사용해 1차원으로 변환
y_predict = y_pred.flatten()
y_predict[:5]
결과값:
array([104.01402 , 139.20187 , 81.99638 , 60.604176, 56.916958],
dtype=float32)
평가
예측한 값을 실제값과 비교하며 평가를 진행한다.
# evaluate를 통해 평가하기
# evaluate가 변수에 할당하는 순서는 모델 compile 때 지정해준 순서대로 할당해준다.
test_loss, test_mae, test_mse = model.evaluate(X_test, y_test)
print("테스트 세트의 loss: {:5.2f}".format(test_loss))
print("테스트 세트의 mae: {:5.2f}".format(test_mae))
print("테스트 세트의 mse: {:5.2f}".format(test_mse))
결과값:
테스트 세트의 loss: 63.63
테스트 세트의 mae: 63.63
테스트 세트의 mse: 11607.33
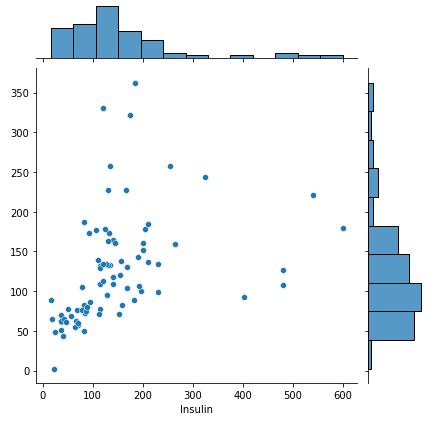
# jointplot 으로 실제값과 예측값을 시각화
sns.jointplot(x = y_test, y = y_predict)
Untitled